Übersicht
Inhaltsverzeichnis
Vorwort
1 Einführung
2 Agile und UML-basierte Methodik
3 Kompakte Übersicht zur UML/P
4 Prinzipien der Codegenerierung
5 Transformationen für die Codegenerierung
6 Grundlagen des Testens
7 Modellbasierte Tests
8 Testmuster im Einsatz
9 Refactoring als Modelltransformation
9.1 Einführende Beispiele für Transformationen
9.2 Methodik des Refactoring
9.3 Modelltransformationen
10 Refactoring von Modellen
11 Zusammenfassung und Ausblick
Literatur
| << zurück | MBSE Home | weiter >> |
9.3 Modelltransformationen
In Abbildung 9.1 wurde eine Definition des Refactorings angegeben, dessen Konzepte in diesem Abschnitt genauer analysiert werden. Dabei werden die Natur von Modelltransformationen, ein Beobachtungsbegriff, ein Transformationskalkül und das Zusammenspiel mit der Semantik der Modellierungssprache diskutiert.
9.3.1 Formen von Modelltransformationen
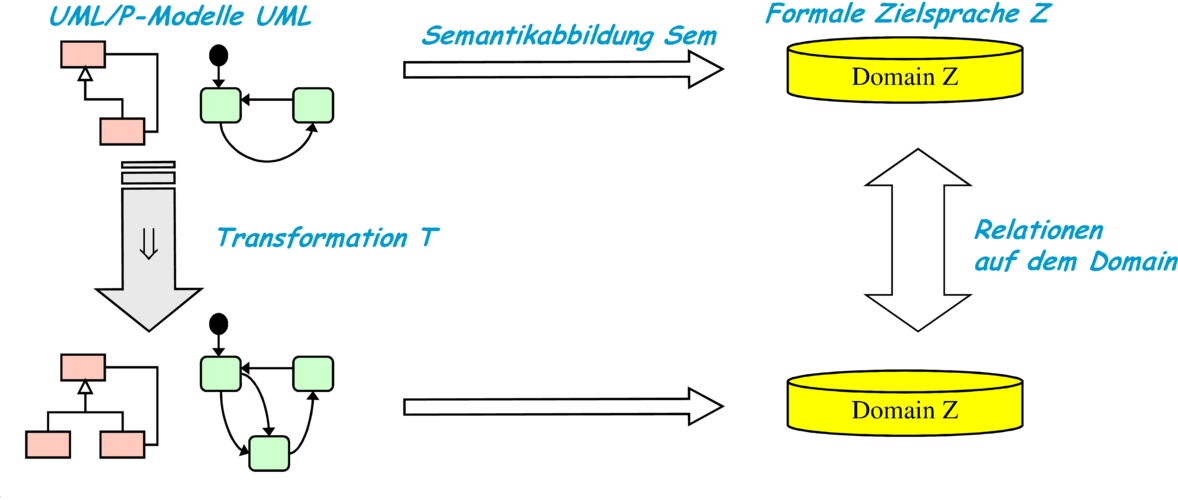
Grundsätzlich ist eine Modelltransformation eine Abbildung ausgehend von einem syntaktisch wohlgeformten Ausdruck der Quellsprache UML/P. Als Zielsprache wird jedoch anders als bei der Codegenerierung nicht Java, sondern wieder die Quellsprache UML/P eingesetzt. Grundsätzlich bleibt aber auch die Vorgehensweise zur Betrachtung der Bedeutung, also der Semantik einer Modelltransformation dieselbe. Abbildung 9.4 beschreibt aufbauend auf Abbildung 4.9 das Grundmuster einer parametrisierbaren Modelltransformation.
- die Modellsprache (UML/P) als eine Menge UML von syntaktisch wohlgeformten Ausdrücken und
- eine Skriptsprache zur Beschreibung der Transformation mit dem Sprachschatz S.
Eine Modelltransformation ist demnach eine Abbildung T : UML → UML. Wird die Modelltransformation mit einem Skript parametrisiert, so entspricht dies einer Abbildung Tp : S × UML → UML.
Tp ist damit eine Art Interpreter der Skriptsprache S für Modelltransformationen. Auf Basis der gelifteten, aber mathematisch äquivalenten Fassung Tp′ : S → UML → UML ist für ein Skript s ∈ S jede Transformation von der Form Tp′(s).
Da Modelltransformationen Abbildungen sind, können ihre funktionalen Eigenschaften untersucht werden. Eine Abbildung kann partiell definiert sein, weil die Voraussetzungen für die Anwendbarkeit der Transformation nicht gegeben sind oder das entstehende neue Modell nicht wohldefiniert ist. Beispielsweise kann eine Unterklasse nur eingefügt werden, wenn die Oberklasse existiert. Soll andererseits eine Klasse eingefügt werden, die bereits existiert, so entsteht ein nicht wohlgeformtes Modell. Wie in diesen beiden Beispielen können viele dieser Voraussetzungen automatisch geprüft werden. Dies ist aber nicht mit allen Voraussetzungen möglich.
Eine Modelltransformation kann injektiv sein. Interessant ist auch der Fall, wenn diese nicht injektiv ist, da dann offensichtlich zunächst unterschiedliche Modelle auf dasselbe neue Modell abgebildet werden und informationstragende Details verloren gehen. Solche Transformationen haben typischerweise Abstraktionscharakter und sind nicht notwendigerweise in allen Details semantikerhaltend. Ein Beispiel ist die Entfernung aller Attribute aus einem Klassendiagramm. So entsteht eine abstraktere Darstellung mit weniger Detailinformation.
Die Surjektivität einer Modelltransformation ist normalerweise nicht gegeben, das heißt nicht jedes Modell wird durch Transformationen erzeugt. Untersuchenswert ist aber bei einem Kalkül, ob die Gesamtheit der zur Verfügung stehenden Modelltransformationen und deren Kombination surjektiv ist. Damit wäre es möglich, aus einem generischen Start, zum Beispiel einem „leeren“ Modell, jedes Modell durch Transformationsschritte zu entwickeln. So werden zum Beispiel beim Delta-Modelling [CHS10, HKR+11a, HKR+11b] Transformationen zum Aufbau von Produktvariabilitäten genutzt.
9.3.2 Semantik einer Modelltransformation
Prinzip der Semantik für eine Transformation
Die Verwendung einer Abbildung statt einer Relation zur Erklärung von Modelltransformationen weist auf den konstruktiven Charakter der Transformation hin. Eine Relation, wie zum Beispiel eine Abstraktions-4
- eine geeignete formale Zielsprache mit dem Sprachschatz Z,
- eine formale Semantik Sem : UML → ℙ(Z), die jedem Element u ∈ UML eine Menge Sem(u) von Elementen der Zielsprache zuordnet.
- Relationen R ⊆ ℙ(Z) × ℙ(Z), die Beziehungen wie Abstraktion, Signaturwechsel, Verfeinerungen, etc. zwischen Elementen der Zielsprache darstellen.
Eine Modelltransformation genügt einer solchen Relation R in Bezug auf ein Modell u ∈ UML, wenn für das transformierte Modell u gilt:
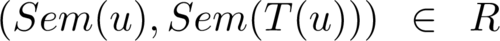
Diese Bedingung lässt sich graphisch durch ein kommutierendes Diagramm illustrieren:
Wenn diese Beziehung für alle Modelle u ∈ UML gilt, für die das transformierte Modell wohlgeformt ist, das heißt u genügt den Kontextbedingungen der Transformation T und T(u) ∈ UML, dann genügt die Modelltransformation der Relation R beziehungsweise ist eine operative Umsetzung von R.
Es gibt typischerweise viele verschiedene Modelltransformationen, die derselben Relation genügen. Wird die Transformation durch ein Skript s ∈ S beschrieben, so genügt ein Skript einer Relation R, wenn die Transformation Tp′(s) der Relation R genügt.
Das in Abbildung 9.5 beschriebene Prinzip der Semantik einer Modelltransformation kann so verstanden werden, dass für die Korrektheit einer Transformation die graphisch dargestellte Kommutativität nachgewiesen wird. Jedoch ist dies in der Praxis insbesondere bei größeren Transformationen nicht ohne weiteres durchführbar. Stattdessen wird dort durch explizite Diskussion von zu beachtenden Sonderfällen und durch Nutzung von Testsammlungen mit Invarianten eine informelle Rechtfertigung für die Transformation gegeben, der formale Nachweis der Korrektheit aber dem gegebenenfalls Ausführenden überlassen. Bei der in Abschnitt 10.1.2 diskutierten Granularität zum Beispiel der Refactoring-Regeln aus [Fow99] aber auch bei der hier gezeigtem Regeln wäre für eine Formalisierung zunächst noch eine deutliche Detaillierung der Kontextbedingungen und der Sonderfälle vorzunehmen. Diese sind zum Beispiel für eine Umsetzung der Refactoring-Regeln in Werkzeuge notwendig. Auf der Basis einer auf diese Weise präzisierten Beschreibung lässt sich dann über die Durchführung von Beweisen zur Korrektheit von Refactoring-Regeln nachdenken.
Beispiele für Semantiken und Relationen
Ein wesentliches Element der Betrachtung der Bedeutung einer Modelltransformation in Abbildung 9.5 ist das Vorhandensein von Relationen R auf der als Semantik verwendeten Zielsprache Z. Je nachdem wie gut die Theorie dort ausgebaut ist, die zu einer als Semantik geeigneten Zielsprache gehört, stehen unterschiedlich mächtige Relationen zur Verfügung. Ein Beispiel für eine ausgereifte Theorie stellen die Ströme in Focus [BS01b] dar, die Abstraktions- und Verfeinerungsrelationen unterschiedlichster Art, von Signatur- bis hin zur Interaktions- und Zeitverfeinerung für verteilte Systeme anbieten.
Ein weiteres Beispiel bilden die in Abschnitt 5.2, Band 1 eingeführten erkennenden Automaten mit einer Semantik in Form von Mengen erkannter Wörter des Eingabealphabets. Wird die erkannte Menge von Wörtern als Beobachtung angenommen, so sind zum Beispiel die aus der Automatentheorie [HU90, Bra84] bekannten Transformationen zur Berechnung einer deterministischen Automatenvariante oder zur Minimierung als Refactorings verstehbar. Auch die meisten Transformationsregeln für Statecharts aus Abschnitt 5.6.2, Band 1 verändern nur die Struktur eines Statecharts, wirken sich aber nicht auf das von außen beobachtbare Verhalten aus.
Bei den Automaten entspricht die Ersetzung eines Eingabezeichens einer Transformation zur Umbenennung der Signatur. Eine Abstraktion auf Signaturebene ist zum Beispiel, wenn eine Gruppe von Eingabezeichen durch ein einzelnes Zeichen ersetzt wird. Abbildung 9.6 zeigt den Effekt einer Abstraktion auf einen erkennenden Automaten.
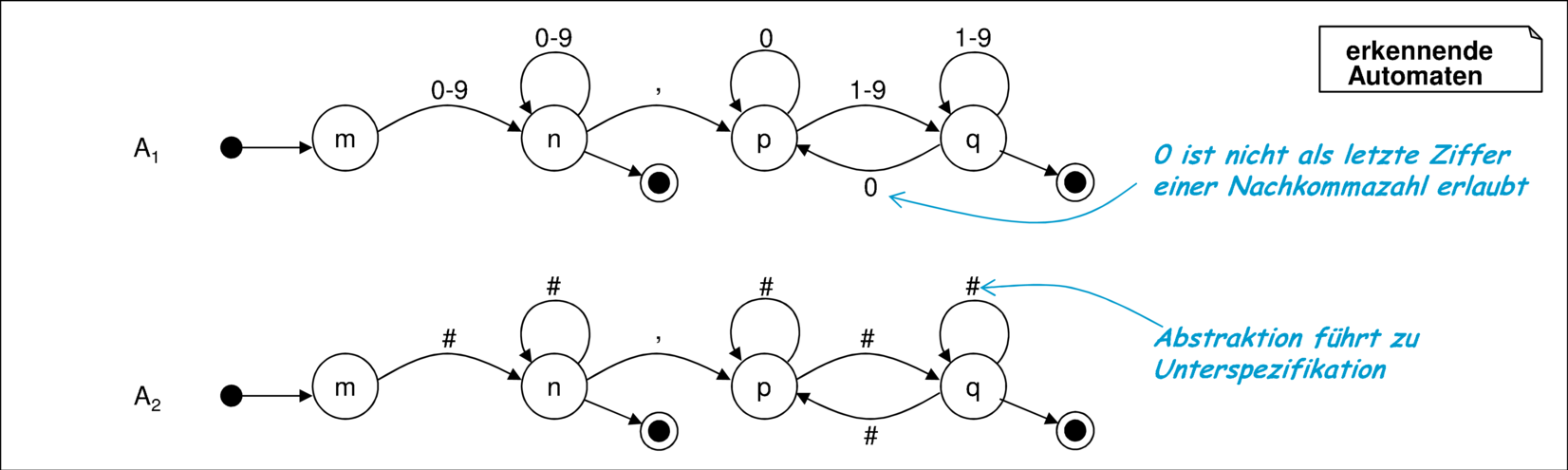
In einer Abstraktion werden die einzelnen Ziffern durch ein Zeichen # ersetzt. Auf dem Alphabet lautet die Abstraktionsrelation
![ϕ = {(n,'#') | n ∈ ['0',...,'9']}](pics/figure247x.png)
Diese wird punktweise auf Wörter ausgedehnt. Beispiel: ('17.33','##.##') ∈ ϕ. Eine Ersetzung der Ziffern im Automat A1 gemäß ϕ führt zu Automat A2.
Es gilt für jedes Wort w1, das von A1 erkannt wird, dass die Abstraktion w2 entsprechend von A2 erkannt wird:
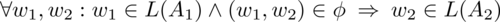
Die Umkehrung gilt jedoch nicht, wie das Beispiel '17.30' zeigt.
Wie bei Abstraktionen häufig der Fall, geht dabei Information verloren. Zum Beispiel können die nur mit der Ziffer 0 markierten Transitionen nicht mehr detailliert genug dargestellt werden. Es entsteht eine gegenüber dem ursprünglichen Automat unterspezifizierte Darstellung, die immer noch wesentliche Informationen enthält, aber nicht mehr so detailliert ist.
Bei echten Abstraktionen geht Information des detaillierten Ausgangsmodells verloren. Es ist daher ein Merkmal von Abstraktionen, dass mehrere Ausgangsmodelle auf dasselbe Zielmodell abgebildet werden. Abstraktionen sind also normalerweise nicht surjektiv. Eine Abstraktion eignet sich daher auch nicht zur Weiterentwicklung eines Modells, sondern zur Analyse oder zur Definition von Tests, die von dem abstrakteren Modell besser abgeleitet werden können.
Beachtenswert ist auch, dass Abstraktion auf der syntaktischen Ebene bedeutet, dass Elemente oder Detailinformation aus dem Modell entfernt werden und das Modell in diesem Sinne „kleiner“ wird. Demgegenüber wird wegen der Form der Semantikdefinition Sem, die, wie in Abschnitt 4.1.1 diskutiert, auch als lose Semantik bezeichnet wird, die Menge von möglichen Implementierungen größer. Die Abstraktionsrelation stellt sich damit als Mengeninklusion dar (formal: R = {(X,Y )|X ⊆ Y }).
Die umgekehrte Relation wird Verfeinerung genannt. Sie erlaubt es, aus einem abstrakten Modell durch das Hinzufügen von Information zu einem konkreteren, detaillierteren und damit auch vollständigeren Modell zu gelangen.
Wie nachfolgend diskutiert, dienen die Refactoring-Techniken der Semantikerhaltung. Sie bilden damit weder Abstraktionen noch Verfeinerungen der Ausgangsmodelle, sondern stellen lediglich eine nach außen nicht beobachtbare Umstrukturierung dar. Die zugehörige Relation wird daher eine Äquivalenz sein, die auf Basis des später eingeführten Beobachtungsbegriffs als Identität wirkt.
Die hier gezeigten Beispiele stammen aus der relativ einfachen und gut verstandenen Theorie endlicher Automaten, weil sich dadurch das Prinzip am besten erklären lässt. Bei den syntaktisch wesentlich reichhaltigeren Statecharts gilt dasselbe Prinzip, aber es sind die zu beachtenden Rahmenbedingungen komplexer. Wesentlich ist bei den Statecharts auch, dass diese eine Ausgabe besitzen, die zusätzlich zur Eingabe beobachtet werden kann. Die sich daraus ergebenden semantikerhaltenden Transformationen für Statecharts wurden in Abschnitt 5.6.2, Band 1 bereits diskutiert.
Kategorien von Semantikrelationen
In den gezeigten Beispielen werden drei semantische Relationen vorgestellt. Eine Kategorisierung zeigt, dass aufgrund der gewählten Semantik auch nur wenige Relationen notwendig sind. Als Kategorien sind identifizierbar:
- Die Abstraktion, die von Details abstrahiert. Das sich ergebende Modell hat als Semantik eine Obermenge des Ausgangsmodells.
- Die Verfeinerung, bei der Details hinzugefügt werden. Verfeinerung ist damit die Umkehrung der Abstraktion.
- Das Refactoring als bezüglich einer vorgegebenen Beobachtung semantikerhaltende Transformation. Refactoring kann gleichermaßen als Spezialfall von Verfeinerung und Abstraktion (bezüglich der Beobachtung) gesehen werden.
- Signaturwechsel durch Umbenennung von syntaktischen Elementen, die in Schnittstellen sichtbar sind.
Die Kategorisierung der semantischen Relationen lässt sich direkt in eine Kategorisierung der Transformationsregeln übertragen. Es gibt also Transformationsregeln für Abstraktion, Verfeinerung, Refactoring und Signaturwechsel, wobei diese Kategorien nicht disjunkt sind. Beispielsweise ist ein Signaturwechsel als Refactoring bezüglich einer Beobachtung auffassbar, die die Signatur nicht beachtet.
Die Ersetzung der Ziffern durch das Zeichen ’#’ in dem Beispiel in Abbildung 9.6 ist eine Abstraktion. Andere Formen von Abstraktionen bestehen darin, Klassen aus einem Klassendiagramm, Objekte aus einem Objektdiagramm, etc. zu entfernen. Das entstehende Modell ist jeweils weniger aussagekräftig. Umgekehrt können in einer Verfeinerung neue Klassen hinzugefügt werden. Ob es sich allerdings um eine echte Verfeinerung handelt, hängt vom nachfolgend diskutierten Beobachtungsbegriff ab.
Transformationen auf Mengen von Artefakten
In Abschnitt 1.4.4, Band 1 wurde festgelegt, dass unter dem Begriff „Modell“ sowohl ein einzelnes Artefakt, also zum Beispiel ein Klassendiagramm oder ein Statechart, als auch eine Sammlung dieser Artefakte zur Beschreibung mehrerer Aspekte verstanden wird. Deshalb werden Modelltransformationen in Abbildung 9.7 auf Mengen von bearbeiteten Artefakten ausgeweitet (eine mit Skripten parametrisierte Form kann analog festgelegt werden). Damit kann zum Beispiel die Umbenennung einer Methode an allen auftretenden Stellen konsistent erfolgen.
Eine Modelltransformation wird erweitert zu einer Abbildung T : ℙ(UML) → ℙ(UML) auf Mengen, indem jedes Artefakt der Menge M ⊆ UML einzeln transformiert wird:
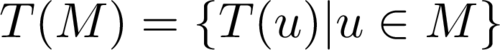
Die Semantikdefinition wird erweitert zu Sem : ℙ(UML) → ℙ(Z), indem für Mengen von Modellen M ⊆ UML, wie bei losen Semantiken üblich, festgelegt wird:
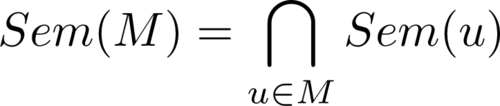
Die Motivation für die in Abbildung 9.7 verwendete Definition der Semantik ist, dass ein Modell u1 als zu erfüllende Bedingung an ein System gesehen werden kann. Es gibt also eine Menge Sem(u1) von Systemen, die die gestellte Bedingung erfüllen. Wird ein zweites Modell u2 als zusätzliche Bedingung aufgestellt, so ergibt sich die Menge von nun als Realisierung infrage kommender Systeme als Sem({u1,u2}) = Sem(u1) ∩ Sem(u2), also genau die Systeme, die beide Bedingungen erfüllen.
Offene und geschlossene Systeme
Die heute übliche Form der Anwendung von Modelltransformationen sowohl bei CASE-Werkzeugen für SDL oder UML-Modelle, als auch bei Entwicklungsumgebungen mit Refactoring-Unterstützung ist die Annahme eines weitgehend geschlossenen Systems.
Ein Modell heißt offen, wenn es ein offenes System modelliert, also explizite Schnittstellen an die Systemumgebung hat, deren Signatur nicht geändert werden kann und über deren Verhalten die Systemumgebung Annahmen macht. Dazu gehören Nachbarsysteme, die zum Beispiel vom Kollegen bearbeitet werden, vorgegebene Frameworks, das Betriebssystem oder Middleware-Komponenten. Ein Modell heißt geschlossen, wenn solche Schnittstellen nicht existieren.
Ein geschlossenes Modell entsteht typischerweise dann, wenn die Umgebung des Systems explizit in dem Modell enthalten ist. Geschlossene Modelle sind leichter zu modifizieren und anzupassen, als offene Modelle, weil in einem offenen Modell die Zusicherungen des Systems gegenüber der Umgebung beibehalten werden müssen. Schnittstellen und Interaktionsmuster dürfen gegenüber der Umgebung nicht verändert werden.
Obwohl in heutigen Systemen zum Beispiel mit Frameworks nahezu immer Schnittstellen zur Umgebung vorhanden sind, wird allgemein versucht, möglichst so zu arbeiten, als würde ein geschlossenes System vorliegen. In dem in [SD00] propagierten und auch in Kapitel 8 verwendeten Ansatz zur Separation des Applikationskerns von externen Komponenten durch Adapter entsteht eine geschlossene Form als Nebeneffekt, indem Schnittstellen zur Umgebung gekapselt werden. Die Adapter werden dann als Teil des Systems behandelt und es entsteht der Effekt eines geschlossenen und damit kontrollier- und manipulierbaren Systems.
Der aus dem methodischen Ansatz des Buchs stammende und in Abschnitt 9.2 diskutierte gemeinsame Modellbesitz für Entwickler hat einen analogen Effekt. So werden Grenzen zwischen den von einem Entwickler selbst erstellten Artefakten und denen der Teamkollegen aufgehoben. Die Umgebung des von ihm primär bearbeiteten Bereichs ist damit für einen Entwickler zugänglich und veränderbar, wie in einem geschlossenen System.
Systemmodell als semantischer Domain
In den Abbildung 9.4 und 9.5 wurden die abstrakten Mengen UML und Z für die Syntax und den semantischen Domain eingeführt. Während die syntaktische Form der UML/P in Band 1 ausführlich diskutiert wurde und im Anhang C, Band 1 durch EBNF-Produktionen und Syntaxklassendiagramme dargestellt ist, wurde der Domain für die Formalisierung der Semantik noch nicht weiter charakterisiert.
Für semantische Domains gibt es eine Reihe von Vorschlägen, die zur Formalisierung von Teilen der UML eingesetzt wurden. [HR00, HR04] enthält dazu eine Übersicht. Zum Einsatz kommen vor allem verschiedene Logiken und mathematische Formalismen, die meistens um spezifische Konstrukte erweitert wurden. Dazu gehört zum Beispiel [BHH+97], in dem eine Formalisierung größerer Teile der UML auf Basis eines verteilten, asynchron kommunizierenden Formalismus diskutiert wurde, oder [FELR98b], in dem eine Transformation in die formale Sprache Z [Spi88] vorgenommen wurde.
Die formale Definition eines semantischen Domains und eine darauf basierende Semantikabbildung ist nicht Teil dieses auf methodische Anwendung der UML ausgelegten Buchs. Dennoch wird in diesem Abschnitt das grundsätzliche Aussehen eines solchen semantischen Domains diskutiert, um damit den Beobachtungsbegriff im nächsten Abschnitt präzisieren zu können.
Um einer Menge von unterschiedlichen UML-Diagrammen eine präzise Semantik geben zu können, müssen in der Semantik alle wesentlichen Aspekte eines Systems dargestellt werden. Es ist nicht ausreichend, einzelne Aspekte, wie das Ein-/Ausgabeverhalten oder die Inhalte einzelner Objekte im semantischen Domain zu modellieren. Stattdessen ist es sinnvoll, eine geschlossene Form eines Systems zu wählen und dessen Struktur und zeitliches Verhalten darzustellen. Wesentlichen Einfluss auf den semantischen Domain haben auch Fragestellungen, ob und in welcher Form Verteilung, Nebenläufigkeit und asynchrone Kommunikation repräsentiert werden sollen. In der in diesem Buch diskutierten Vorgehensweise werden solche Aspekte nur am Rand behandelt. Auch die in Kapitel 8 definierten Tests für verteilte Systeme und parallele Threads ersetzen echte Nebenläufigkeit durch simuliertes Scheduling und damit einem sequentiellen, deterministischen Ablauf.
Bereits [Huß97, Rum96] beschreiben die grundlegende Struktur solcher semantischen Domains, die auch als so genanntes Systemmodell, also einer abstrakten Darstellung der Struktur und des Verhaltens von Systemen, bezeichnet wird. Detailliert ausgeführt ist ein Systemmodell für die UML in [BCGR09a, BCGR09b]. Grundsätzlich ist eine solche mathematisch formale Darstellung inhaltlich sehr ähnlich zur Definition einer virtuellen Maschine, wie sie in Abschnitt 4.2 für die UML diskutiert wurde. Für die Definition einer virtuellen Maschine wird jedoch eine konstruktiv, operationelle Beschreibung angegeben, während ein Systemmodell als denotationelle Semantik im Allgemeinen kompakter definiert werden kann.
Ein für die UML/P adäquates Systemmodell beschreibt ein System über eine Menge von Systemabläufen, die ihrerseits Interaktionen, Snapshots und die darin enthaltenen Objekte charakterisieren. Abbildung 9.8 charakterisiert als Vereinfachung von [BCGR09a, BCGR09b] wesentliche Elemente, wobei vereinfachend auf unendliche Abläufe verzichtet wird und die eigentlich den Threads zugeordneten Stacks auf die Objekte verteilt werden.
- Ein Objekt o = (ident,attr,stack) besitzt einen Identifikator ident, zu jedem Zeitpunkt eine Belegung attr : VarName → Value und dem ihm zugeordneten Anteil aus dem Stack. Obj sei die Menge der Objekte.
- Ein Snapshot sn ⊆ Obj ist eine Sammlung von Objekten, die zu einem Zeitpunkt existieren. Die Links zwischen Objekten werden durch die im Snapshot eindeutigen Identifikatoren dargestellt. SN sei die Menge der Snapshots.
- Die Menge der Aktionen Act beschreibt Methodenaufrufe, Returns, Attributzuweisungen, etc.
- Aus einem Snapshot lässt sich erkennen, welches Objekt gerade aktiv ist und damit welche Aktion als nächstes durchgeführt wird. Der Programmzähler ist also aus dem stack der Objekte abstrahierbar. Damit ist die nächste stattfindende Aktion eines Snapshots festgelegt: act : SN → Act.
- Ein Ablauf run ∈ SN* ist eine Reihe von zeitlich aufeinander folgenden Snapshots.
- Das Systemmodell SM ⊆ SN* besteht aus einer Menge von Abläufen.
Eine Reihe von zusätzlichen Bedingungen sind notwendig, um SM auf die Abläufe einzuschränken, die tatsächlich auftreten können. Beispielsweise ist der Kontrollfluss zu wahren und nur Attribute im Objekt zu belegen, die dort auch existieren.
In Abbildung 9.5 wurde als abstrakte Zielsprache für eine Semantikdefinition Z eingeführt. Konkret kann Z = SM gesetzt werden. Jedes UML-Artefakt u ∈ UML erhält dann seine Semantik in Form einer Teilmenge von Systemabläufen aus SM , die die beschriebenen Eigenschaften erfüllen.
9.3.3 Beobachtungsbegriff
Nach der Charakterisierung der Transformation einer Refactoring-Regel ist die zu erhaltende Beobachtung des Verhaltens wesentlich. In den beiden am meisten beachteten Werken zum Thema Refactoring [Fow99, Opd92] wird aber der Beobachtungsbegriff nicht präzisiert. In [Opd92, S. 28] wird der Beobachtungsbegriff auf die Relation zwischen Ein- und Ausgabe reduziert, ohne Interaktionen zu berücksichtigen. In [Fow99] wird an die intuitive Vorstellung der Beobachtung durch den Anwender appelliert. Als Beobachtung wird in XP-Projekten vor allem das an der Anwenderschnittstelle beobachtbare Verhalten verstanden. Die Schnittstellen zu anderen Systemen, Datenbanken, Frameworks, etc. gehören aber unter Umständen ebenfalls zum „extern beobachtbaren Verhalten“.
Obwohl der Beobachtungsbegriff im XP-Ansatz nicht präzisiert wurde, gibt es eine Möglichkeit, Beobachtungen zu definieren, um damit das Refactoring eines Systems zu prüfen. Der XP-Ansatz nutzt dazu Testfalldefinitionen, die in Java formuliert werden und sich weitgehend auf die Prüfung des Ergebnisses in Form einer Nachbedingung beschränken.
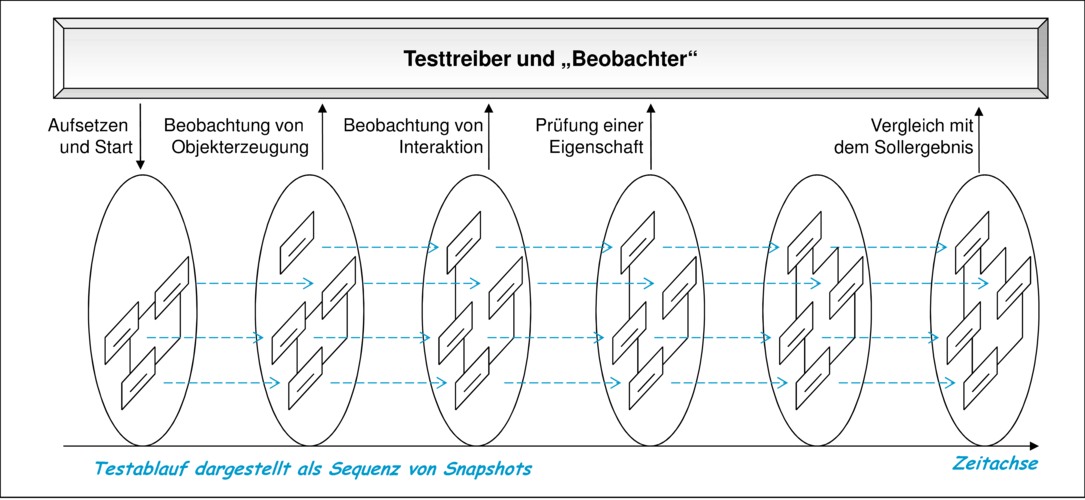
Die in den Kapiteln 6 und 8 diskutierten Tests und insbesondere ihre deskriptiven Bestandteile, wie Orakelfunktionen, Invarianten, Interaktionsmuster und Nachbedingungen, sind ein ideales Mittel zur Darstellung von Beobachtungen. Es ist daher sinnvoll, die Beobachtungen bei Refactorings durch in UML/P formulierte Testfälle zu modellieren. Anhand der aufgezählten Liste von Darstellungsformen ist ersichtlich, dass sich eine mit der UML/P formulierte Beobachtung nicht auf Schnittstellen beschränken muss, sondern auch interne Interaktionsmuster, Zwischenzustände und den Endzustand des Testlings „beobachten“ kann. Abbildung 9.9 illustriert dies auf Basis eines Systemablaufs bestehend aus einer einer Sequenz von Snapshots.
Die Möglichkeit, im Test jegliche Kapselung eines Testlings zu durchbrechen, birgt wesentliche Vorteile bei der Modellierung von Tests, da so nicht erst aufgrund des Ausgabeverhaltens Rückschlüsse auf den Zustand des Testlings geschlossen werden müssen, sondern der Zustand direkt zugänglich ist. Auch die Modellierung von Interaktionsmustern innerhalb einer Teilkomponente, die aus mehreren Objekten besteht, bricht die Kapselung der Komponente auf. Der Nachteil solcher Tests besteht darin, dass diese auch kleine Änderungen des Testlings registrieren, indem sie entweder nicht mehr kompilierbar sind (zum Beispiel bei Signaturänderung) oder ein Scheitern des Testlaufs anzeigen (zum Beispiel bei Änderung des Interaktionsmusters). Dies bedeutet zusätzlichen Aufwand beim Refactoring, da diese Tests ebenfalls angepasst werden müssen.
Es ist daher bei der Definition von Tests sorgfältig abzuwägen, ob die Interna des Testlings oder eine abstraktere Programmierschnittstelle genutzt werden. In der Praxis sind zwei grobe Klassen von Tests identifizierbar. Die Unit-Tests für einzelne Methoden und Klassen werden normalerweise auf Interna zugreifen und müssen gemeinsam mit dem Code modifiziert werden. Vom Anwender formulierte und mithilfe von Entwicklern realisierte, automatisierte Tests sind hingegen Teil der Beobachtung durch einen Anwender. Derartige Tests sollten durch Refactorings nicht beeinträchtigt werden. Dies bedeutet aber, dass ein solcher Test möglichst gegen eine abstrakte Schnittstelle testet, die auch dann beibehalten wird, wenn Interna des Systems modifiziert werden. Im Detail bedeutet dies, dass es für Akzeptanztests besser ist, nach Möglichkeit
- Query-Methoden statt direkte Attributzugriffe zu verwenden,
- OCL-Eigenschaften zu verwenden, die erlauben gewisse Freiheiten zu formulieren, statt Attributwerte präzise vorzugeben,
- im Sollergebnis unwichtige Objekte und Attribute zu ignorieren und sich auf die wesentlichen Ergebnisse zu konzentrieren sowie
- nur wesentliche Interaktionen zu beobachten.
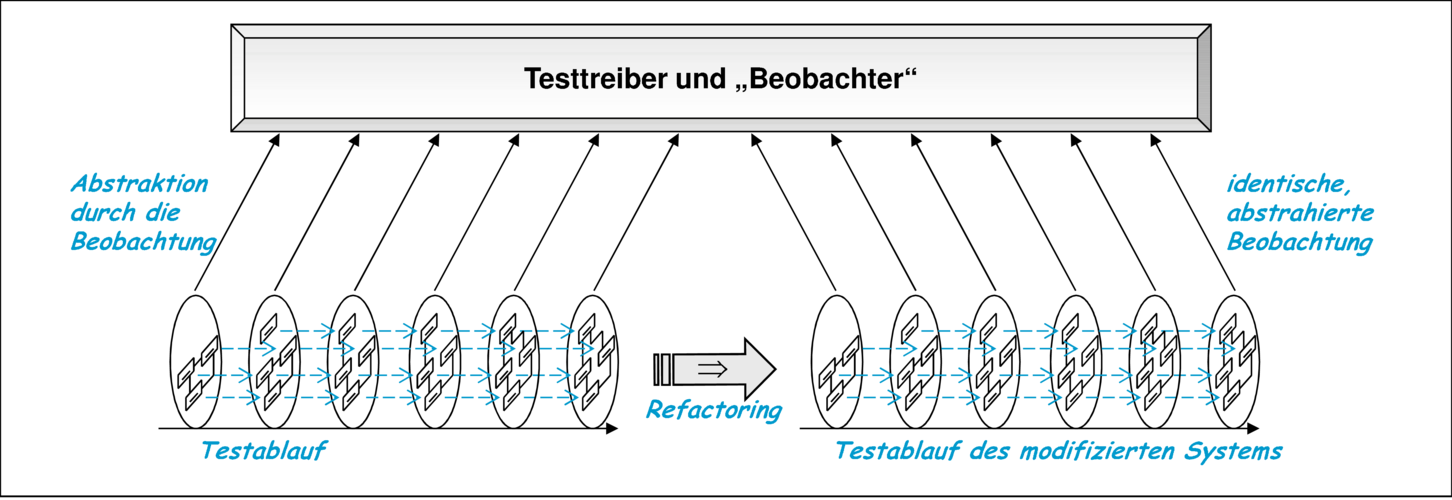
Auf diese Weise enthält die durch den Test definierte Beobachtung eine Abstraktion und erlaubt damit unterschiedlichen Abläufen, den Test zu erfüllen. Das System beziehungsweise sein Modell kann damit in gewissen Grenzen modifiziert werden, ohne dass sich dadurch die abstrakte Beobachtung ändert. Dies kann wie in Abbildung 9.10 illustriert werden.
Ein Nebeneffekt der Nutzung von Abstraktion bei der Beobachtung eines Testablaufs ist allerdings, dass ein Test nicht alle Aspekte des Testlings prüft. So kann ein Codestück zwar ausgeführt worden sein, sein Effekt aber durch den Test vernachlässigt werden. Als Konsequenz daraus ist die Aussagekraft von Überdeckungsmetriken für Tests, die auf Prüfung durchlaufenen Codes basieren, möglicherweise beschränkt. Hilfreich sind hier Mutationstests [Voa95, KCM00, Moo01], die prüfen, ob eine Änderung des Codes zu einer Erkennung veränderten Verhaltens durch die vorhandene Testsammlung führt. Damit wird gemessen, inwieweit die grundsätzlich abstrahierenden Beobachtungen einer Testsammlung in ihrer Gesamtheit das beobachtbare Verhalten erfassen.
Nach diesen aus der Praxis heraus motivierten und graphisch illustrierten Überlegungen zur Darstellung von Beobachtungen wird nun die im vorherigen Abschnitt begonnene Präzisierung von Modelltransformationen in Abbildung 9.11 um einen Beobachtungsbegriff erweitert. In dieser Abbildung wird außerdem ein Kontext für Transformationen eingeführt. Der Kontext besteht aus Modellen, auf die das transformierte Modell zum Beispiel durch Nutzung der darin definierten Typen aufbaut, die selbst aber nicht verändert werden. Ein Beispiel ist ein Klassendiagramm, das einem zu transformierenden Objektdiagramm zugrunde liegt.
- Eine Beobachtung besteht aus einem oder mehreren Artefakten der UML/P.
- Die Semantik einer Beobachtung ist die Teilmenge der durch die Beobachtung erlaubten Abläufe des Systems Z und damit ebenfalls durch Sem : UML → ℙ(Z) festgelegt.
- Sei u ∈ UML ein Modell, das zum Beispiel zur konstruktiven Codegenerierung verwendet und durch b ∈ UML beobachtet wird. Die Beobachtung von u bezieht sich dann nur auf die gemeinsamen Abläufe, dargestellt durch Sem(u) ∩ Sem(b).
- Eine Modelltransformation T(u) auf dem Modell
u ∈ UML ist beobachtungsinvariant bezüglich einer
Beobachtung b ∈ UML, wenn der beobachtete Ausschnitt identisch ist:
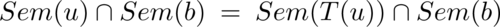
- Wird die Modelltransformation auf mehrere Artefakte A ⊆ UML angewandt und
im Kontext anderer Modelle K ⊆ UML betrachtet, so gilt die Beobachtungsinvarianz bezüglich einer Menge von Beobachtungen B ∈ UML,
wenn gilt:
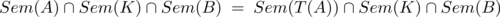
In derselben Weise kann die in Abschnitt 9.3.1 diskutierte Verfeinerung in einen Kontext und relativ zu einer Beobachtung präzisiert werden:
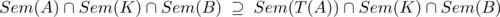
Bei einer Abstraktion T wird entsprechend die umgekehrte Relation ⊆ genutzt.
Der dritte Punkt der Definition in Tabelle 9.11 drückt aus, dass eine Beobachtung in Form eines Tests den Testling zu bestimmten Systemabläufen zwingt und nur dort prüft. Sem(u) ∩Sem(b) stellt entsprechend diese von beiden Modellen durchführbaren Abläufe dar. Entsprechend ist die Beobachtungsinvarianz nur bezüglich der durch Sem(b) beschriebenen Abläufe notwendig. Dies gibt der Transformation die Freiheit, unbeobachtete, also typischerweise interne Modifikationen vorzunehmen.
Alternativ kann die Semantik von Beobachtungen auch durch die Einführung eines semantischen Domains B und einer Abstraktionsfunktion β : Z → B beschrieben werden. Eine Beobachtung wird dann durch b ∈ B repräsentiert und charakterisiert eine Äquivalenzklasse von Abläufen {z ∈ Z|β(z) = b}. Verändert also ein Refactoring einen Ablauf z nach z′, so muss der beobachtbare Anteil jedoch gleich bleiben: β(z′) = β(z). Ein Nachteil dieses Ansatzes sind die Notwendigkeit zur Definition einer adäquaten Menge von Beobachtungen B.
Wie der letzte Punkt in Abbildung 9.11 zeigt, existiert formal kein Unterschied zwischen dem Kontext und den Beobachtungen. Ein solcher Kontext kann zum Beispiel aus unveränderbaren Schnittstellen zur GUI, Datenbanken, etc. bestehen. Er kann aber auch die von der aktuellen Bearbeitung nicht betroffenen Modelle beinhalten.
Ein Beispiel für eine Beobachtung ist etwa eine in OCL formulierte Methodenspezifikation. Ihre Semantik ist ein Prädikat über den Beschreibungen von Abläufen SM aus Abbildung 9.8. Ein Ablauf erfüllt die Methodenspezifikation genau dann, wenn die Nachbedingung zum Ende jedes Methodenaufrufs gilt, bei dessen Beginn die Vorbedingung erfüllt war.5
Ein vollständiger Test, bestehend aus Testdatensatz, Testtreiber, etc., stellt ebenfalls ein Prädikat über einen Systemablauf dar. Ein Systemablauf erfüllt einen Test genau dann, wenn der Test erfolgreich durchgeführt wurde. Das heißt, es gibt in dem Ablauf einen Snapshot, der dem initialen Testdatensatz entspricht, der Testling wird ausgeführt und die geforderten Bedingungen und Interaktionen sind während beziehungsweise nach dem Test erfüllt.
9.3.4 Transformationsregeln
In der Theorie ist eine Transformationsregel als Abbildung UML → UML erklärt, die bei Bedarf auf Mengen von UML-Artefakten zur simultanen Anwendung erweitert werden kann. In der Praxis können jedoch unterschiedlichste Ausprägungen dieser Abbildung existieren. Die Anzahl der möglichen Regeln hängt von der syntaktischen Reichhaltigkeit der zugrunde liegenden Sprache ab. Die UML/P besitzt zwar deutlich weniger Sprachkonzepte als der UML-Standard [OMG10], ist aber immer noch eine eher große Modellierungssprache. Ausgehend von Erfahrungen mit Transformationskalkülen anderer Sprachen muss damit gerechnet werden, dass die Anzahl möglicher und sinnvoller Regeln mehr als linear mit der Größe der Sprache wächst. Ein Grund dafür ist, dass viele Regeln das Zusammenspiel mehrerer Sprachkonzepte behandeln. Es ist daher praktisch unmöglich, für die UML/P einen vollständigen Regelkalkül zu identifizieren. Dies ist aber auch für den praktischen Einsatz nicht notwendig. Wesentlich ist vielmehr, eine anwendbare Sammlung kompakter und einfacher Regeln zur Verfügung zu haben.
Die Anzahl und konkrete Form von Transformationsregeln hängt sehr oft von der Ausprägung der zugrunde liegenden Sprache ab. Aber es gibt auch allgemeine Prinzipien für Transformationsregeln, die weitgehend auf alle Sprachen angewandt werden können. Dazu gehören zum Beispiel die Expansion von Methoden oder die Migration von Attributen, die auch bei prozeduralen Sprachen wie C auf Funktionen und struct-Einträge angewandt werden können. Die Regelanwendungen unterscheiden sich jedoch in ihren technischen Details. Bei der Methodenexpansion sind in Java Sonderfälle für abstrakte Methoden, dynamische Bindung, statische Methoden oder Konstruktoren zu berücksichtigen oder die Exceptions sind speziell zu behandeln.
Die anwendbaren Regeln sollten möglichst einfach und generalisiert sein, um so maximale Anwendbarkeit sicherzustellen. Die Mächtigkeit eines Regelkalküls besteht zum Großteil aus der Komponierbarkeit der Regeln, indem diese etwa hintereinander angewandt werden. Mithilfe von zielgerichteten Taktiken können aus einfachen Regeln komplexe Transformationen komponiert werden. Damit lässt sich zum Beispiel die Einführung eines Entwurfsmusters aus [GHJV94] als Serie einfacher Transformationsregeln erklären [TB01].
Wesentlich ist dabei, dass für die grundlegenden Transformationsregeln Werkzeugunterstützung zur Verfügung steht, die auch die Kontextbedingungen prüft und die Wohlgeformtheit des Ergebnisses sichert. Zielgerichtete Taktiken können als Skripte analog zu der in Abschnitt 4.2.3 bereits für die Codegenerierung diskutierten Form realisiert werden.
Eine Reihe von Transformationsregeln sind außerdem nur in Anwesenheit bestimmter Stereotypen anzuwenden. In Band 1 ist beispielsweise demonstriert, wie Transitionen mit überlappenden Schaltbereichen unterschiedlich priorisiert sein können und dementsprechend verschiedene Regeln anwendbar sind. Weil aber die in UML/P verfügbaren Stereotypen mit dem in Abschnitt 2.5.3, Band 1 beschriebenen Verfahren frei erweitert werden können, ist es notwendig, gemeinsam mit der Einführung eines neuen Stereotyps entsprechende Transformationsregeln und Skripte zu definieren, die einen spezialisierten Umgang mit Modellen mit diesem Stereotyp erlauben.
9.3.5 Korrektheit von Transformationsregeln
Wie bereits in den vorherigen Abschnitten anhand von Beispielen illustriert, besitzt eine Transformationsregel meistens Kontextbedingungen, die erfüllt sein müssen, um die Korrektheit einer Transformation zu sichern. Diese Kontextbedingungen können verschiedener Bauart sein, weshalb eine Klassifizierung von Transformationsregeln anhand der Art der Kontextbedingungen sinnvoll ist.
Die Kontextbedingungen reichen von einfachen und meistens syntaktisch prüfbaren Einschränkungen bis hin zu komplexen, nicht mehr automatisch entscheidbaren Invarianten.
- Im einfachsten Fall besitzt eine Transformation keine Kontextbedingungen.
- Einfache syntaktische Bedingungen wie zum Beispiel, dass ein zu ersetzender Ausdruck eine Variable nicht verwendet, können durch entsprechende Prüfungen automatisiert werden. Diese Form der Kontextbedingungen tritt häufig auf und kann durch eine gute Werkzeugunterstützung anhand des Syntaxbaums effizient geprüft werden.
- Komplexere Kontextbedingungen wie etwa die Typkorrektheit lassen sich ebenfalls anhand der Syntax entscheiden, erfordern aber erheblich mehr Aufwand. Weitere Beispiele für solche Bedingungen sind Kontrollflussanalysen, zum Beispiel um die Unerreichbarkeit von Zuständen im Statechart oder von Anweisungen im Methodenrumpf zu identifizieren, oder Datenflussanalysen, um sicherzustellen, dass Variablen vor ihrer Nutzung belegt werden, wie sie beispielsweise in modernen Compilern integriert sind.
- Nicht automatisiert überprüfbare Bedingungen sind meist komplexere Beziehungen zwischen Elementen des Systems. Beispielsweise können mehrere Attribute einer Klasse in einem inneren Zusammenhang stehen, der durch eine OCL-Bedingung formulierbar ist. Auf Basis dieses Zusammenhangs kann ein Attribut gegebenenfalls durch ein anderes ersetzt werden. Die Korrektheit von OCL-Bedingungen ist aber im Normalfall nicht automatisch prüfbar, sondern erfordert punktuelle Tests oder interaktive Verifikation.
Die Kategorie der syntaktisch prüfbaren Kontextbedingungen wird im Compilerbau typischerweise in die Unterkategorien (einfache, kontextfreie) syntaktische und (komplexere, später durchgeführte) semantische Analyse getrennt. Beide Formen werden aber auf Basis der Syntax vorgenommen und werden automatisiert durchgeführt.
Für manche Fragestellungen existiert nur ein semi-entscheidbares Verfahren, bei dem unter Umständen die Gültigkeit der Kontextbedingung nicht entschieden werden kann. In diesem Fall wird die Kontextbedingung bereits zurückgewiesen, wenn sie nicht positiv entschieden werden konnte. Dabei spielt fast immer die bereits bei der Entwicklung von Testfällen in Kapitel 7 diskutierte Problematik der Unentscheidbarkeit der Erfüllbarkeit boolescher Aussagen oder eine praktisch nicht mehr immer berechenbare, exponentielle Komplexität bei der Entscheidungsfindung eine Rolle.
Mehrere oft auftretende Rahmenbedingungen sind bereits aus anderen Ansätzen zur transformationellen Softwareentwicklung bekannt:
- Terminierung
- Eine Kontextbedingung kann fordern, dass die Berechnung eines Ausdrucks immer terminiert. Auch eine Exception ist eine Terminierung. Wie bereits in Kapitel 3, Band 1 diskutiert, ist die Terminierung durch Tests insbesondere mit gegebenen Schleifen-Invarianten und Terminierungsbedingungen relativ einfach prüfbar, obwohl sie im Prinzip unentscheidbar ist. Für praktisch relevante Transformationen kann aber davon ausgegangen werden, dass jeder Ausdruck terminiert oder die zur Verfügung stehenden Tests eine Nichtterminierung entdecken.
- Definiertheit
- Eine Berechnung ist definiert, wenn sie immer terminiert und dabei ein normales Ergebnis, also keine Exception erzeugt.
- Determiniertheit
- Eine Berechnung ist determiniert, wenn sie immer terminiert und dabei ein eindeutiges Ergebnis produziert. Dies kann durchaus eine Exception sein. Wesentlich ist, dass bei der Berechnung kein Zufallselement auftritt oder sich zumindest nicht auf das Ergebnis auswirkt. Diese Bedingung kann zum Beispiel durch Einbeziehung von Zeitabfragen verletzt werden. Wie in Abschnitt 3.3.4, Band 1 an der Konversion von Mengen in Listen mit dem OCL-Operator asList diskutiert, ist das Ergebnis dieses Operators zwar eindeutig, aber dem Entwickler nicht a priori bekannt. Der Vorteil dieser Festlegung ist, dass einerseits ein Ausdruck der Form set.asList determiniert ist, andererseits aber einem OCL-Interpreter die konkrete Umsetzung überlassen bleibt.
- Seiteneffektfreiheit
- Ein Seiteneffekt einer Berechnung ist eine permanente Zustandsänderung der vorhandenen Objektstruktur, indem zum Beispiel eine lokale Variable, ein Attribut oder ein Link verändert wurde. Die Erzeugung neuer Objekte ist, wie in Abschnitt 3.4.1, Band 1 besprochen, nur dann ein Seiteneffekt, wenn dieses Objekt von der ursprünglichen Objektstruktur aus zugänglich gemacht wird.
Kontextbedingungen, die semantische Äquivalenzen beinhalten, sind oft unentscheidbar. Zum Beispiel ist bei der Ersetzung eines Ausdrucks durch einen anderen, wie in der Beispielregel in Abschnitt 9.1, deren Gleichheit nicht automatisiert prüfbar. Die Darstellung einer solchen Eigenschaft erfolgt beispielsweise durch OCL-Bedingungen. Diese Bedingungen können daher nur für Tests oder für die Verifikation eingesetzt werden. Während Tests keine Gewissheit über die Korrektheit einer OCL-Bedingung geben, sind sie doch effizienter zu bewerkstelligen als die tatsächliche Verifikation.
Für die Verifikation einer solchen Invariante ist es meistens notwendig, den Code mit weiteren Invarianten zu versehen und ähnlich der Hoare-Logik alle Einzelschritte zu verifizieren (eine Java-Variante ist zum Beispiel in [vO01] zu finden). Für Systeme höchster Qualität oder besonders kritische Bereiche, kann dies insbesondere in Kombination mit Tests sinnvoll sein. Durch Tests werden zunächst vorhandene Fehler erkannt und eliminiert. Mit Verifikationstechniken wird dann die vollständige Korrektheit bewiesen und jedes Restrisiko einer fehlerhaften Invariante ausgeschaltet. Durch die Vorschaltung der Tests kann Verifikationsaufwand für viele der fehlerhaften Aussagen eingespart und so effizienter vorgegangen werden.
Für viele Systeme wird aber die Verwendung von Tests ausreichend sein. Wie in Abschnitt 10.2 anhand einer Vorgehensweise für Datenstrukturwechsel gezeigt, können Tests nicht nur als Indikator für die Korrektheit eines Systems, sondern auch für die Korrektheit einer Transformation eingesetzt werden.
9.3.6 Ansätze der transformationellen Softwareentwicklung
Einige Ansätze transformationeller Softwareentwicklung sowie eine interessante Diskussion über dessen Auswirkungen sind in [Pep84, Kap. 5] enthalten. Darin werden unter anderem die Fragen nach der Semantik, der Nützlichkeit von Top-Down-Darstellungen einer Softwareentwicklung und der Sprachunabhängigkeit von Transformationstechniken diskutiert.
Transformationelle Softwareentwicklung
Insbesondere in der theoretischen Informatik wurden bereits eine Reihe von transformationellen und auf Verfeinerungskonzepten basierende Ansätze vorgestellt. Dazu gehören zum Beispiel Arbeiten von Dijkstra [Dij76], Wirth [Wir71], Bauer [BW82], Back [BvW98] und Hoare [HHJ+87]. CIP-L [BBB+85] ist zum Beispiel eine Sprache, die einen algebraischen Spezifikationsstil sowie funktionale, algorithmische und prozedurale Programmierstile in sich vereint und durch zahlreiche transformationelle Schritte von einem in den nächsten Sprachstil überleiten kann. Als Methodik wurde diesem Top-Down-Transformationsansatz zugrunde gelegt, dass zunächst in einer abstrakten Spezifikationssprache modelliert, dann in eine funktionale Sprache transformiert und letztendlich mit dem Ziel einer prozeduralen Implementierungssprache optimiert wird. Elemente dieses Ansatzes transformationeller Softwareentwicklung sind auch im heutigen, an der inkrementellen Vorgehensweise orientierten Refactoring wieder zu finden. Dazu gehört zum Beispiel das Konzept, Optimierungen am Code erst möglichst spät durchzuführen, wenn die Korrektheit geklärt und die Stabilität der Funktionalität gesichert sind. In [BBB+85] wurde wie auch in verwandten Ansätzen die Verifikation als Mechanismus zur Sicherung der Korrektheit einer Transformation verwendet. Diese wird im hier vorgeschlagenen Ansatz durch die weniger aufwändigen Tests abgelöst.
Der Ansatz zur Spezifikation und Transformation von Programmen in [Par90] enthält ebenfalls eine detaillierte Sammlung von Regeln zur transformationellen Softwareentwicklung für abstrakte, durch algebraische Gesetze definierte Datentypen, funktionale und imperative Programme sowie von Datenstrukturen. Dort werden zum Beispiel die Entfernung überflüssiger Zuweisungen und Variablen, die Umordnung von Anweisungen, die Behandlung von Kontrollstrukturen oder verschiedene Varianten der Komposition von Funktionen diskutiert, die teilweise eine direkte Entsprechung in [Fow99] finden. Darüber hinaus bietet [Par90] wie auch [BBB+85] Techniken zur inkrementellen Verfeinerung einer Spezifikation in Richtung auf eine operationelle Implementierung.
Algebraische Spezifikation
In den algebraischen Spezifikationstechniken wurde als erstes die Definition expliziter Beobachtungen eingeführt. Mithilfe des Versteckens von Sorten hat zum Beispiel OBJ [FGJM85] einen Mechanismus angeboten, Details eines algebraisch spezifizierten abstrakten Datentypen zu kapseln und eine explizite nutzbare und beobachtbare Schnittstelle zur Verfügung zu stellen. Weitere algebraische Ansätze [ST87, BHW95, GR99, BFG+93] demonstrieren, dass es möglich ist, explizit extern sichtbares Verhalten zu definieren und darauf rigorose Beweistechniken anzusetzen. [BBK91] enthält eine generelle Übersicht über Ansätze zur Definition von Beobachtbarkeit in algebraischen Spezifikationen.
Wie bereits diskutiert, ist es ein gewisser Nachteil des hier verwendeten, aber dafür sehr flexiblen Testansatzes, dass die Beobachtung und damit auch die beobachtete Schnittstelle durch die Tests nur implizit und für jeden Test anders definiert ist. Es erfordert daher die Disziplin des Testentwicklers insbesondere bei Akzeptanztests möglichst auf stabile und wie bei den algebraischen Spezifikationen explizit „publizierte“ Schnittstellen zuzugreifen.
Refactoring und Verifikation
In [Sou01] werden Refactoring und Verifikation in Beziehung gesetzt. In diesem Sinne wird zunächst die Verifikation mittels einer unter Umständen interaktiv erstellten Sammlung von Beweisen als wesentliches Element zur Sicherstellung der Korrektheit eines Systems eingesetzt. Die Weiterentwicklung des Systems mithilfe kleiner, systematischer Schritte führt dann dazu, auch die Beweise entsprechend zu adaptieren und deren Korrektheit durch automatische Wiederholung sicherzustellen. Durch adäquate Werkzeugunterstützung, wie sie zum Beispiel Isabelle [NPW02] mit den teilweise sehr mächtigen Beweistaktiken bietet, kann so eine evolutionäre Weiterentwicklung unter Wiederverwendung von Verifikationsanteilen vorgenommen werden.
Transformation graphischer Spezifikationen
Eine Reihe von Arbeiten zeigt, dass für graphische Spezifikationen, unabhängig davon, ob sie Struktur-, Verhaltens- oder Interaktionssichten eines Systems darstellen, ebenfalls transformationelle Techniken entwickelt werden können. Der in [BS01b] beschriebene Ansatz Focus demonstriert die Kombinierbarkeit formaler, textbasierter Spezifikationstechniken mit einer graphischen Repräsentation der verteilten Interaktion von Komponenten. Darin stehen präzise Techniken zur Dekomposition von Komponenten und Kanälen und zur Verfeinerung von Verhalten und Schnittstellen bereit, deren Auswirkungen an graphischen Modellen geplant und studiert werden können.
In diesem Kontext wurde in [PR97, PR99] eine Technik zur Glas-Box-Transformation der inneren Struktur eines verteilten Systems vorgestellt, dessen an der Schnittstelle beobachtbares Verhalten bei der Transformation äquivalent bleibt oder verfeinert wird. Ein Teil dieser Transformationstechnik basiert auf der Verhaltensverfeinerung innerer Komponenten, die zum Beispiel mit Zustandsautomaten beschrieben werden können [Rum96].
Dass diese Transformationsformen nicht nur für massiv verteilte oder Hardware-nahe Systeme geeignet sind, zeigt [RT98] in der Geschäftsprozesse durch strukturelle Transformationen optimiert werden.
Zusammenfassung
Zusammenfassend lässt sich feststellen, dass das semantikerhaltende Refactoring auf einem durch eine Testsammlung basierenden Beobachtungsbegriff basiert. Zwei Verallgemeinerungen, der Transformation von Modellen, die Abstraktion und insbesondere die Verfeinerung könnten nicht nur zur Restrukturierung der vorhandenen Systembeschreibung, sondern auch zur transformationellen Weiterentwicklung dienen. Ansätze wie die in Abschnitt 9.3.6 beschriebenen [BBB+85, Par90] haben dies gezeigt. Praktisch anwendbar werden transformationelle Entwicklungsschritte aber vor allem durch die Existenz automatisierter Tests.
9.3.7 Transformationssprachen
Um Transformationen der genannten Arten flexibel einsetzen zu können, ist eine eigenständige Sprache für die Definition von Transformationen notwendig. Nur so können Transformationen explizit definiert werden.
So werden in der Mathematik Ersetzungsregeln in Form von Gleichungen definiert. Die Gleichungssprache der Mathematik ist damit auch für die Definition von Ersetzungen nutzbar. In den formalen Methoden werden Ersetzungsregeln unter anderem benutzt, um Typisierungsregeln in Form eines Kalküls anzugeben, wie in CIP [BBB+85, BEH+87], um algebraische Umformungen von textuellen Programmier- und Spezifikationssprachen zu definieren oder wie in Isabelle [NPW02, Pau94], um Theoreme mit Anwendungsbedingungen als anwendbare Transformationen anzugeben. Die Ersetzungsregeln der Mathematik sind Teil der „Mathematischen Sprache‘“ selbst, während die Kalkülsprachen von Isabelle/HOL oder CIP jeweils eigene Teilsprachen darstellen, die mit der transfomierten Basissprache harmonisch zusammenpassen.
Graph Grammatiken [Nag79, NS91] bilden als Analogon zu textuellen Grammatiken zunächst die Möglichkeit Graphstrukturen zu definieren und eignen sich besonders, um die typischerweise (im mathematischen Sinn) als Graphen definierte Struktur vom UML-Modellen in Werkzeugen zu speichern. Transformationen für Graphen können darauf aufsetzend zum Beispiel mittels Graphersetzungssystemen [Sch88, Sch91, LMB+01], algebraischen Ansätzen [EEPT06, Tae04] oder einer Notation zu ihrer Steuerung mittels Fujaba’s „Story Diagrams“ [FNTZ00] definiert werden. Das Graphersetzungssystem PROGRES [Sch91, Zün96] beinhaltet nicht nur Graphmatching-Techniken, sondern auch eine komplexe Steuerung zur Ausführung und zum Backtracking von Ersetzungsregeln. Das Konzept der Triple Graph Grammars [Sch94] erlaubt auch die Transformation von Graphen zwischen unterschiedlichen Strukturen, so dass damit auch eine Übersetzung zwischen Modellen verschiedener Sprachen möglich wird (etwa von Automaten zu Java).
Ein weiterer Ansatz zur Definition von Transformationen auf Modellen nutzt Metamodelle in Form vom Objektstrukturen. Hier werden Klassendiagramme ähnlich wie in Kapitel C, Band 1 eingesetzt, um die abstrakte Syntax zu definieren. Auf den dadurch definierten Objektstrukturen lassen sich dann Transformationen auf der abstrakten Syntax unter Umgehung der konkreten, für den Nutzer lesbaren Repräsentation der Modelle definieren. Transformationssprachen wie ATL [JK05], MOLA [KCS05], BOTL [MB03] oder die Epsilon Transformation Language [KRP11] nutzen diesen Ansatz, der häufig auf EMF [SBPM08] basiert. In [CH06] findet sich eine gute Klassifikation über diese Art von Transformationssprachen. Die OMG hat unter dem Namen „Query View Transformation (MOF QVT)“ eine Spezifikation für solche Transformationssprachen definiert [OMG08] auf der mittlerweile auch Graphersetzungssysteme wie MOFLON [AKRS06, WKS10] aufbauen.
Während Metamodelltechniken aber auch manche Graphtransformationsansätze [LKAS09] vor allem auf die generische, sprachunabhängige Definition von Transformationen setzen, versuchen andere in Analogie zur Mathematik eine möglichst nahe an der zugrundeliegenden Modellierungssprache ausgerichteten Transformationssprache zu entwickeln [BW06, Grø09a, RW11]. Der Vorteil einer Transformationssprache auf Basis der konkreten Syntax besteht darin, dass der Anwender sich leichter in eine solche Transformationssprache hinein findet und diese daher eher nutzt, als wenn ihm diese Transformationssprache völlig unbekannt ist oder er sich mit der abstrakten Syntax der von ihm benutzten Modellierungssprachen auseinander setzen muss.
Die Auswahl einer geeigneten Transformationssprache und dazu gehörender Werkzeuge zur Definition von Refactorisierungsschritten ist notwendig, um die im nachfolgenden Kapitel 10 behandelten Transformationen festzulegen. Wesentliche Einflussfaktoren sind hier natürlich auch die bereits bisher eingesetzten Werkzeuge.
Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012
| << zurück | MBSE Home | weiter >> |