Übersicht
Inhaltsverzeichnis
Vorwort
1 Einführung
2 Agile und UML-basierte Methodik
3 Kompakte Übersicht zur UML/P
4 Prinzipien der Codegenerierung
5 Transformationen für die Codegenerierung
6 Grundlagen des Testens
7 Modellbasierte Tests
8 Testmuster im Einsatz
9 Refactoring als Modelltransformation
10 Refactoring von Modellen
10.1 Quellen für UML/P-Refactoring-Regeln
10.2 Additive Methode für Datenstrukturwechsel
10.3 Zusammenfassung der Refactoring-Techniken
11 Zusammenfassung und Ausblick
Literatur
| << zurück | MBSE Home | weiter >> |
10.2 Additive Methode für Datenstrukturwechsel
Refactoring-Schritte sind relativ klein und systematisch, um sicherzustellen, dass die Regelanwendung beherrschbar ist und eventuell auftretende Fehler effizient erkannt und behoben werden können. In diesem Abschnitt wird eine Alternative diskutiert, die die Durchführung komplexerer Refactoring-Schritte ohne Zerlegung in Einzelschritte besser beherrschbar macht. Diese Technik eignet sich besonders für den Wechsel von Datenstrukturen, die mit Klassendiagrammen modelliert werden. Sie basiert auf der im Auktionsprojekt entwickelten und mehrfach erfolgreich angewandten Idee, die alte und die neue Datenstruktur während der Umformung parallel zu nutzen und durch geeignete Invarianten miteinander in Beziehung zu setzen. Weil dabei zunächst die neue Datenstruktur hinzugefügt wird, ohne die alte zu entfernen, wird die Vorgehensweise als additiv bezeichnet. Nachfolgend wird zunächst die Vorgehensweise vorgestellt und dann anhand zweier Beispiele demonstriert und im Detail diskutiert.
10.2.1 Vorgehensweise für den Datenstrukturwechsel
Refactoring-Schritte sind dazu geeignet, einen Datenstrukturwechsel vorzunehmen und dabei die Korrektheit der Modifikation soweit wie möglich durch Tests sicherzustellen. In formaleren Ansätzen wie [BBB+85] sind gerade Datenstrukturwechsel eine gut verstandene Vorgehensweise, deren Kontextbedingungen mit Verifikationstechniken sichergestellt werden. In Anlehnung an die dort entwickelten Konzepte, wird in Tabelle 10.10 eine pragmatische Vorgehensweise zum Wechsel einer Datenstruktur vorgeschlagen. Die Verwendung von Invarianten zur Festlegung der Beziehungen zwischen der alten und der neuen Datenstruktur ist dabei ein wesentlicher Baustein der korrekten Transformation.
|
|
|
|
Additive Vorgehensweise zum Datenstrukturwechsel
|
|
|
|
|
|
Problem, Ziel und Motivation |
Das Zerlegen eines Datenstrukturwechsels in viele kleine Refactorings ist nicht immer einfach und birgt durch die größere Anzahl an Schritten das Risiko des Einbaus eines Fehlers. Ziel ist es, unter Verwendung von Invarianten, die die alte und die neue Datenstruktur in Beziehung setzen, größere Refactoring-Schritte beherrschbar zu machen und zusätzliche Sicherheit bei der Durchführung zu erhalten. |
|
|
|
|
Vorgehens-weise |
Die Durchführung eines Datenstrukturwechsels mit Refactoring-Techniken besteht aus folgenden Schritten:
|
|
|
|
|
Beispiele |
In den Abschnitten 10.2.2 und 10.2.3 wird die Vorgehensweise anhand zweier Beispiele aus dem Auktionssystem demonstriert. |
|
|
|
|
Beachtenswert |
|
|
|
|
|
Tabelle 10.10.: Additive Vorgehensweise zum Datenstrukturwechsel
|
|
Der Trick bei dieser Vorgehensweise besteht darin, im Gegensatz zu einem Verifikationsansatz die Invarianten in Tests einzusetzen. Unter der Annahme, dass eine ausreichende Testsammlung für das System existiert, kann die Korrektheit der Transformation so mit höherer Wahrscheinlichkeit sichergestellt werden. Da die zur Prüfung des Datenstrukturwechsels notwendigen Tests in der in diesem Buch vorgeschlagenen Vorgehensweise bereits existieren, ist der Datenstrukturwechsel effizient durchführbar. Tatsächlich wurde dieses Prinzip im Auktionsprojekt mehrfach mit außerordentlichem Erfolg eingesetzt und der für komplexere Datenstrukturwechsel geschätzte Aufwand drastisch unterschritten, weil systematisch vorgegangen wurde, dabei wenig Fehler entstanden sind und diese sehr schnell identifiziert, lokalisiert und behoben werden konnten.
Ist das Zutrauen in die Korrektheit der Transformation immer noch nicht ausreichend, so kann wie bereits in Abschnitt 10.1.4 diskutiert nach Durchführung der Tests zusätzlich eine Verifikation zum Beispiel mit einer der Hoare-Logik nachempfundenen Vorgehensweise vorgenommen werden.
Das in Tabelle 10.10 skizzierte Vorgehen zum Wechsel einer Datenstruktur ist in Abhängigkeit der tatsächlichen Komplexität und Form der Datenstruktur jeweils geeignet anzupassen. Werden zum Beispiel Elemente der alten Datenstruktur als Methodenparameter eingesetzt, so ist durch Erweiterung der Methodenparameter (Schritt 2) die neue Datenstruktur parallel hinzuzufügen. Dadurch entsteht die Möglichkeit, in den Vorbedingungen derartiger Methoden die Übereinstimmung beider Datenstrukturen zu prüfen (Schritt 3). In einem weiteren Refactoring-Schritt werden am Ende die nicht mehr benötigten Methodenparameter der alten Datenstruktur entfernt (Schritt 7).
Neben der Entfernung der alten Datenstruktur in Schritt 7 zeigen sich bei der Vereinfachung der Berechnungen in Schritt 6 die Vorteile der neuen Datenstruktur. Natürlich lassen sich die Schritte 5 und 6 auch verschränkt durchführen. Um die Beziehungen zwischen beiden Datenstrukturen effektiv beschreiben zu können, kann es sinnvoll sein, vorübergehend zusätzliche Methoden zur Übersetzung zwischen den Datenstrukturen zu verwenden und diese am Ende ebenfalls zu entfernen.
Obwohl sich diese Vorgehensweise bei nahezu allen Refactoring-Regeln, wie zum Beispiel dem Verschieben eines Attributs oder der Teilung einer Klasse, einsetzen lässt, bietet sich diese Technik vor allem für größere Refactorings an. Nachfolgend wird anhand zweier Beispiele aus dem Auktionsprojekt ausschnittsweise gezeigt, wie diese Vorgehensweise angewandt werden kann.
10.2.2 Beispiel: Darstellung von Geldbeträgen
In einer ersten Version des Auktionssystems wurden Geldbeträge durch eine Zahl des Datentyps long dargestellt. Für die Internationalisierung war das Systems auf Money-Objekte umzustellen, die unterschiedliche Währungen innerhalb einer Auktion verarbeiten können. Nachfolgend wird eine vereinfachte Form der Datenstrukturen umgestellt.1
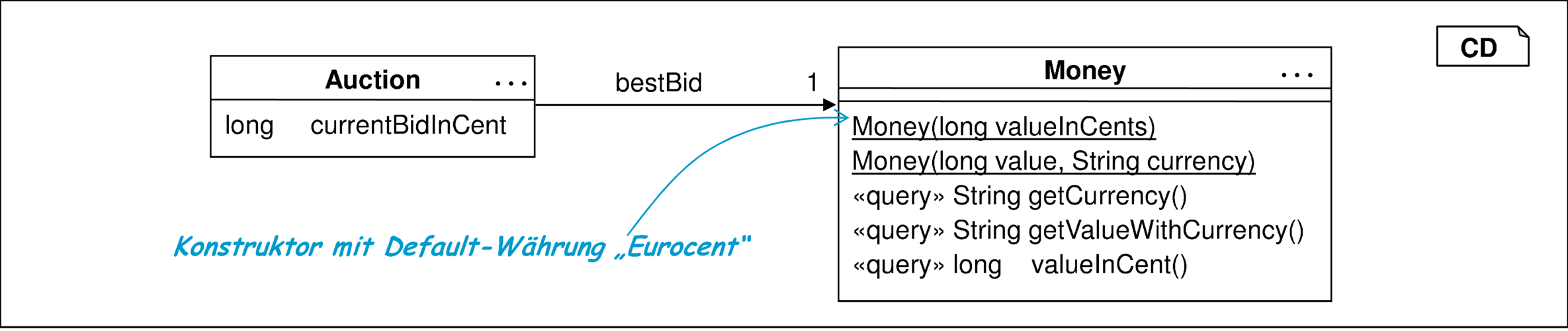
Schritt 1: Die Ausgangsdatenstruktur wird, wie in Abbildung 10.11 dargestellt, identifiziert.
Schritt 2: Die neue Datenstruktur ist in Abbildung 10.12 dargestellt. Für die neue Klasse Money werden außerdem geeignete Tests entwickelt, die die von der Klasse angebotenen Funktionen ausreichend testen.
Schritt 3: Invarianten zwischen beiden Datenstrukturen sind leicht zu identifizieren. Mithilfe der zur Verfügung gestellten Query valueInCent kann als Invariante festgelegt werden:
OCL  context Auction a inv BestBidEqualsCurrentBid: context Auction a inv BestBidEqualsCurrentBid: |
| currentBidInCent == bestBid.valueInCent() |
Entsprechend der in der UML/P verwendeten zweiwertigen Logik für OCL und dem Umgang mit undefinierten Werten, ist die Invariante genau dann erfüllt, wenn die Assoziation bestBid besetzt ist und das Money-Objekt den entsprechenden Inhalt besitzt.
Schritt 4: Die neue Datenstruktur ist zwar eingeführt, wird aber noch nicht eingesetzt. In diesem Schritt wird sie deshalb an allen Stellen besetzt beziehungsweise modifiziert, an denen dies auch mit der alten Datenstruktur geschieht. Ein Auszug aus der Methode, die ein Gebot annimmt und das neue Bestgebot berechnet, ist in Abbildung 10.13 angegeben.
Da die gezeigte Methode das aktuelle Gebot als Argument erhält, wird ein zweites Argument für die neue Darstellung des Gebots eingeführt. Die erste OCL-Bedingung ist aus der Invariante BestBidEqualsCurrentBid abgeleitet und sichert die Korrektheit der Argumente. Die anderen beiden OCL-Bedingungen testen die Invariante zu Beginn der Methode und nach der Veränderung des Money-Objekts.
Schritt 5: Die neue Datenstruktur wird nun besetzt, aber es wird noch immer die alte benutzt. Deshalb werden jetzt alle Stellen ersetzt, die die alte Datenstruktur verwenden. Dazu können oft die Invarianten eingesetzt werden. In diesem Fall kann die unter Schritt 3 formulierte Invariante BestBidEqualsCurrentBid direkt als Ersetzungsanweisung verstanden werden. Die linke Seite der Gleichung
OCL  currentBidInCent == bestBid.valueInCent() currentBidInCent == bestBid.valueInCent() |
kann an allen benutzenden Stellen durch die rechte Seite der Gleichung ersetzt werden. Abbildung 10.14 zeigt dies an der Weiterentwicklung des Ergebnisses aus Schritt 4 (Abbildung 10.13).
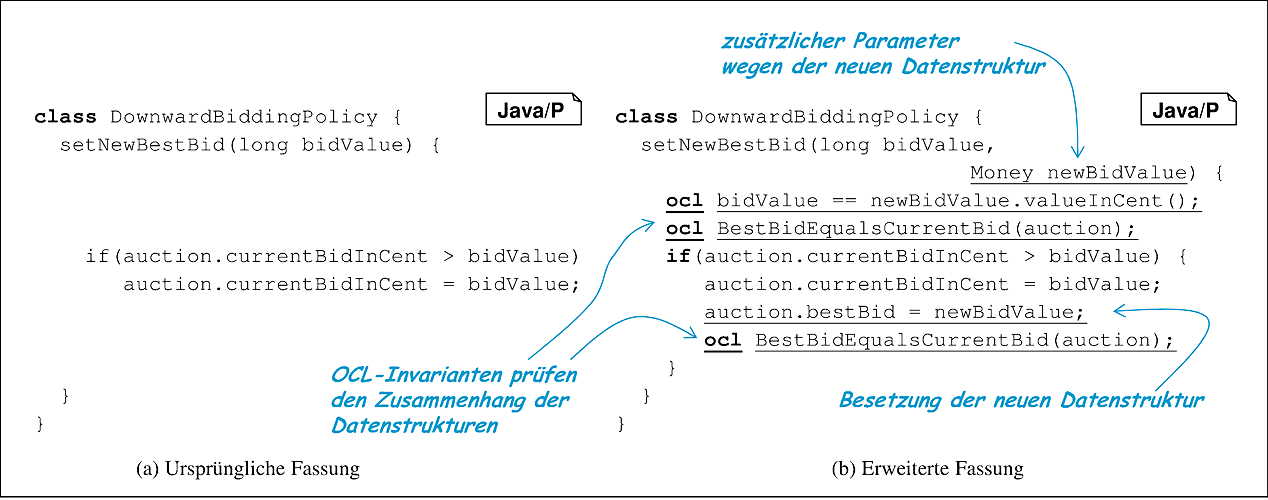
Diese Transformation ist auch für die OCL-Bedingungen sinnvoll. Zum Beispiel kann die Spezifikation der Methode setNewBestBid entsprechend Abbildung 10.15(a) zunächst zu der in (b) dargestellten Form erweitert und dann zu der Fassung in (c) transformiert werden. Bei diesen Transformationen ist allerdings zu beachten, dass die Invarianten, die für die Darstellung des Zusammenhangs der alten mit der neuen Datenstruktur eingesetzt werden, nicht ebenfalls ersetzt werden.
Dieses Beispiel zeigt auch, dass die Umsetzung nicht immer völlig schematisch ablaufen kann. In diesem Fall wird zum Beispiel ein Attribut durch einen Methodenaufruf ersetzt und der Operator @pre ist nicht mehr anwendbar. Deshalb wird der entsprechende Wert in einer let-Variable zwischengespeichert.
Schritt 6: Die Vereinfachung der entstandenen Codestücke und insbesondere der Ausdrücke ist ein wesentlicher Schritt, um den entstandenen Code lesbar und elegant zu halten. Tatsächlich werden die Schritte 5 und 6 oft verschränkt durchgeführt. Schritt 6 kann aber bei großen Datenstrukturwechseln auch in mehrere kleine Schritte aufgeteilt werden. Beispielsweise gilt die Ersetzung:

Ebenso können Berechnungen vereinfacht werden, wobei bei der nachfolgenden Transformation darauf zu achten ist, dass Seiteneffekte entstehen, wenn das alte bid1-Objekt noch an anderer Stelle bekannt ist:

Wesentlich ist hier, wie auch bei allen anderen Schritten, dass danach die automatisierten Tests durchgeführt werden. Sollten nicht ausreichend Tests vorhanden sein, so sind bei Bedarf zusätzliche Tests zu entwickeln.
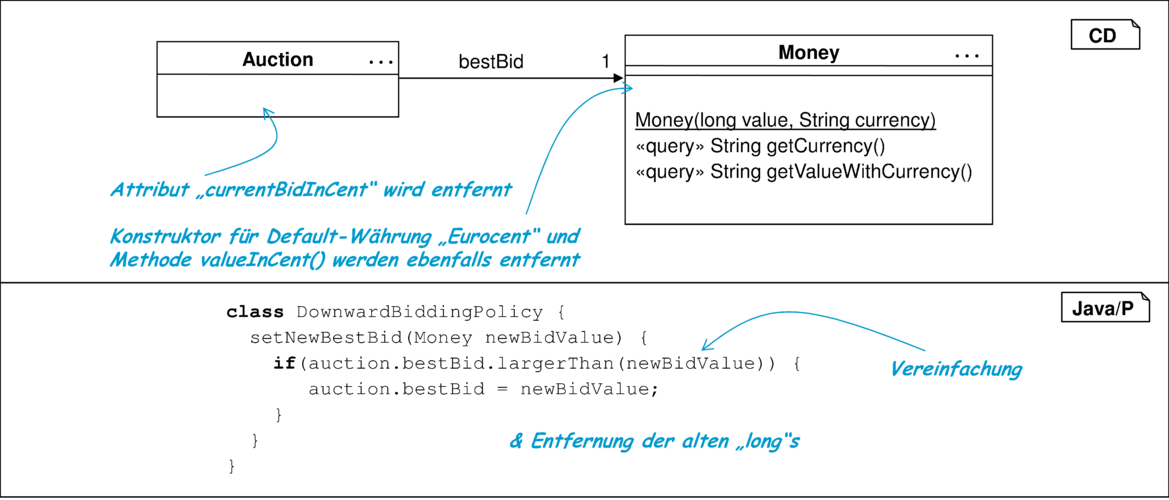
Schritt 7: Im letzten Schritt lassen sich nun die alte Datenstruktur sowie alle Invarianten und Bedingungen, die die alte und neue Datenstruktur in Beziehung setzen, entfernen. Es entsteht das in Abbildung 10.16 gezeigte Ergebnis.
Für das gezeigte einfache Beispiel ist die verwendete Methode relativ komplex und aufwändig. Die hier vorgeschlagene, sehr detaillierte Methode empfiehlt sich erst, wenn der Wechsel komplexer und damit fehleranfälliger wird. Dabei muss es sich nicht notwendigerweise um komplexe Datenstrukturen handeln. Es ist auch bereits hilfreich, diese Technik anzuwenden, wenn viele Attribute des Typs long durch Money-Objekte ersetzt werden sollen und die Komplexität damit durch die Menge zu ersetzender Elemente entsteht.
10.2.3 Beispiel: Einführung des Chairs im Auktionssystem
Das additive Verfahren wurde im Auktionssystem in dieser Detailliertheit zum ersten Mal angewandt, als die Anforderungen auftraten, (1) dass ein Bieter an mehreren Auktionen gleichzeitig teilnehmen kann, und (2) dass ein Kollege, der eine Auktion beobachtet, nicht notwendigerweise vom gleichen Unternehmen wie der Bieter stammen muss.
Anforderung (1) war eigentlich von Beginn an bekannt, wurde jedoch nicht sofort umgesetzt, da aufgrund der kurzen Laufzeit von Auktionen mehrere parallele Auktionen für denselben Bieter zunächst unwahrscheinlich waren. Dies änderte sich, als zeitlich synchronisierte Auktionen ähnlicher Güter zur Verbesserung der Konkurrenzsituation gewünscht wurden.
Schritt 1: Identifikation der alten Datenstruktur
Das Auktionssystem war von Anfang an dafür ausgelegt, neben den aktiven Bietern und dem Auktionator, den Kunden weitere, in Anhang D, Band 1 beschriebene Rollen für Beobachter anzubieten. Dabei waren mehrere Varianten externer Beobachter zugelassen. So genannte Bieter-Kollegen erhalten alle Informationen des eigentlichen Bieters, haben aber nicht die Möglichkeit zur Gebotsabgabe. Die Erkennung von Kollegen wurde über ein gemeinsames Company-Objekt realisiert. Anforderung (2) stammt aus der Erkenntnis, dass große Unternehmen unterschiedliche Standorte und Subunternehmen haben, externe Consultants als Bieter anstellen, etc. und deshalb eine Flexibilisierung notwendig war.
Das beschriebene Beispiel wurde mit der in diesem Abschnitt skizzierten Vorgehensweise sehr effizient und fehlerfrei umgesetzt. Dies ist umso erstaunlicher, als aufgrund der zentralen Bedeutung der geänderten Systemstruktur nicht nur der Applikationskern, sondern auch die Datenbank, die Ergebnissicherheit, das System zum Aufsetzen von Auktionen und die graphische Oberfläche bis hin zum auf der Firmenzugehörigkeit basierenden Passwort-geschützten Anmeldeverfahren anzupassen waren. Dies implizierte aber auch die Änderung einer Reihe von Unit- und Akzeptanztests.
In Abbildung 10.17 wird ein vereinfachter Ausschnitt der Ausgangssituation zur Änderung des Applikationskerns dargestellt.

OCL  // Nur ein Bieter pro Unternehmen // Nur ein Bieter pro Unternehmen |
| context Person p1,p2 inv OneBidderOnly: |
| p1.company==p2.company implies |
| !p1.isBiddingAllowed || !p2.isBiddingAllowed |
OCL  // Personen desselben Unternehmens sind in der gleichen Auktion // Personen desselben Unternehmens sind in der gleichen Auktion |
| context Person p1,p2 inv SameAuction: |
| p1.company==p2.company implies p1.auction==p2.auction |
OCL  // Personen desselben Unternehmens haben // Personen desselben Unternehmens haben |
| // gleiches Symbol und Eigengebot |
| context Person p1,p2 inv SameInfos: |
| p1.company==p2.company implies |
| p1.graphSymbol==p2.graphSymbol |
| && p1.ownBid==p2.ownBid |
Die letzte OCL-Bedingung SameInfos zeigt, dass mehrere identische Informationen, wie das aktuelle eigene Gebot, das zur Darstellung verwendete Symbol, etc. redundant gepeichert wurden.
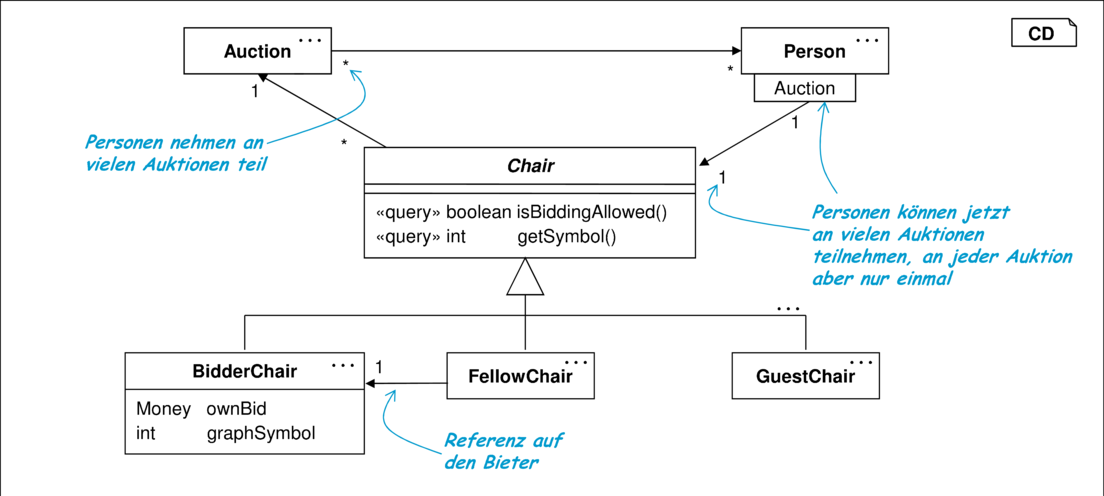
Schritt 2: Entwicklung der neuen Datenstruktur
Als erwünschte Datenstruktur wurde die Situation in Abbildung 10.18 identifiziert, in der die Rollen nicht mehr durch ein Flag, sondern durch Unterklassen festgelegt werden. Außerdem wurde die Abstraktion Chair als Metapher für den Stuhl einer Person in einer klassischen Auktion eingeführt.
Java/P  class BidderChair { class BidderChair { |
| isBiddingAllowed() {return true;} |
| getSymbol() {return graphSymbol;} |
| } |
| class FellowChair { |
| // Keine Gebotsabgabe, ansonsten Delegation |
| isBiddingAllowed() {return false;} |
| getSymbol() {return bidderChair.getSymbol();} |
| } |
| class Guest { |
| isBiddingAllowed() {return false;} |
| getSymbol() {return Symbol.GUEST_WITHOUT_OWN_BIDS;} |
| } |
OCL  // FellowChair und BidderChair sind in der gleichen Auktion // FellowChair und BidderChair sind in der gleichen Auktion |
| context FellowChair cc inv ChairSameAuction: |
| cc.auction == cc.bidderChair.auction |
OCL  // Assoziation Auction - Person - Chair stimmt // Assoziation Auction - Person - Chair stimmt |
| context Auction a inv ChairAssoc1: |
| forall p in a.person: |
| p.chair[a].auction==a |
| context Person p inv ChairAssoc2: |
| forall a in p.chair.keySet(): |
| p.chair[a].auction==a |
Die ursprünglichen Bedingungen OneBidderOnly und SameInfos fallen weg. SameAuction wird zu ChairSameAuction. Neu eingeführt wurden die Invarianten ChairAssoc1 und ChairAssoc2, die die Rolle der Klasse Chair in Bezug auf die Assoziation zwischen Person und Auction demonstrieren. Gemeinsam mit der Einführung der Chair-Klassen wurden eine Reihe von neuen Tests für die neue Datenstruktur entwickelt, die hier aber nicht dargestellt werden.
Schritt 3: Festlegung der Invarianten
Die beiden Klassendiagramme in den Abbildungen 10.17 und 10.18 zeigen jeweils nur Teile der Implementierung, die sich in den Klassen und einer Assoziation überlappen. Die Klassendiagramme werden jetzt gemeinsam als Implementierung genutzt, indem, wie in Abschnitt 2.4, Band 1 beschrieben, eine Verschmelzung der Diagramme zur Codegenerierung eingesetzt wird. Darauf aufbauend lassen sich nun die notwendigen Invarianten zwischen der alten und der neuen Datenstruktur identifizieren. Dabei wird zunächst weiter davon ausgegangen, dass Personen nur an einer Auktion teilnehmen, denn die Tests sind für die alte Datenstruktur ausgelegt:
OCL  context Person p inv: context Person p inv: |
| // zunächst nur ein Chair für jede Person |
| p.chair.size==1; |
Dementsprechend ist any p.chair das eindeutige Chair-Objekt, das einer Person zugeordnet ist. Damit lassen sich einige Invarianten identifizieren, die den Transfer der Informationen vom Person- zum Chair-Objekt betreffen.
OCL  context Person p inv PersonChairInvs: context Person p inv PersonChairInvs: |
| let Chair c = any p.chair in |
| // Bieter hat BieterChair |
| ( p.role==IS_SUPPLIER && p.isBiddingAllowed <=> |
| c instanceof BidderChair ) && |
| // Bieter-Kollege hat FellowChair |
| ( p.role==IS_SUPPLIER && !p.isBiddingAllowed <=> |
| c instanceof FellowChair ) && |
| // isBiddingAllowed stimmt überein |
| p.isBiddingAllowed == c.isBiddingAllowed() && |
| // Symbol stimmt überein |
| p.graphSymbol == c.getSymbol() |
Folgende Eigenschaften gelten zusätzlich, sind aber separat dargestellt, um sie einzeln benennen zu können:
OCL  context Person p inv BidderChairInv: context Person p inv BidderChairInv: |
| let Chair c = any p.chair in |
| // Gebot stimmt bei Bietenden überein |
| typeif c instanceof BidderChair |
| then p.ownBid == c.ownBid |
| else true |
OCL  context Person p inv FellowChairInv: context Person p inv FellowChairInv: |
| let Chair c = any p.chair in |
| // Gebot stimmt bei Bieter-Kollegen überein |
| typeif c instanceof FellowChair |
| then p.ownBid == c.bidderChair.ownBid |
| else true |
Die Verbindung des Bieter-Kollegen zum zugehörigen Bieter wird über einen Link organisiert. Wenn Person p1 bieten darf und Person p2 einen Bieter-Kollegen derselben Company darstellt, dann muss der Link entsprechend gesetzt sein:
OCL  context Person p1, Person p2 inv: context Person p1, Person p2 inv: |
| let BidderChair c1 = (BidderChair) any p1.chair; |
| FellowChair c2 = (FellowChair) any p2.chair in |
| defined(c1) && defined(c2) && p1.company==p2.company |
| implies c2.bidderChair==c1 |
Die neue Datenstruktur ist genügend komplex, um die Fehlerfreiheit während der Entwicklung der neuen Datenstruktur und der Invarianten illusorisch zu machen. Aber durch den effektiven Einsatz von Syntaxprüfungen und automatisierten Tests lassen sich die so entstandenen Modelle gegenseitig prüfen. Fehler werden aufgrund der mehrfachen Redundanz der dargestellten Systemeigenschaften
- in den automatisierten Tests,
- in der alten als korrekt angenommenen Datenstruktur,
- in der neuen Datenstruktur sowie
- durch die Verbindung beider Datenstrukturen durch Invarianten erkannt.
Schritt 4: Besetzung der neuen Datenstruktur
Im nächsten Schritt wird an allen Stellen der Code zur Besetzung der neuen Datenstruktur eingebaut und dabei werden diese Invarianten benutzt, um die Korrektheit des neuen Codes zu prüfen. Da die Invarianten bereits vorhanden sind, können diese als anleitende Spezifikation eingesetzt werden, die beschreiben wie die Implementierung anzupassen ist. Zum Beispiel kann aus p.graphSymbol==c.getSymbol() die Implementierung für getSymbol() extrahiert werden. Dadurch werden die Überlegungen bei der Definition der Invarianten wiederverwendet und so die Effizienz der Entwicklung gesteigert. Wenn die Invarianten allerdings zur Ableitung der Implementierung eingesetzt werden, dann werden fehlerhafte Invarianten nicht erkannt, sondern wirken sich im Gegenteil auch durch eine fehlerhafte Implementierung aus. Es ist daher fallbasiert zu überlegen, die Implementierung unabhängig von den Invarianten durchzuführen, denn es existieren für die alte Datenstruktur Tests, die später auf die neue Datenstruktur umgesetzt werden und dann die Korrektheit der neuen Datenstruktur prüfen.
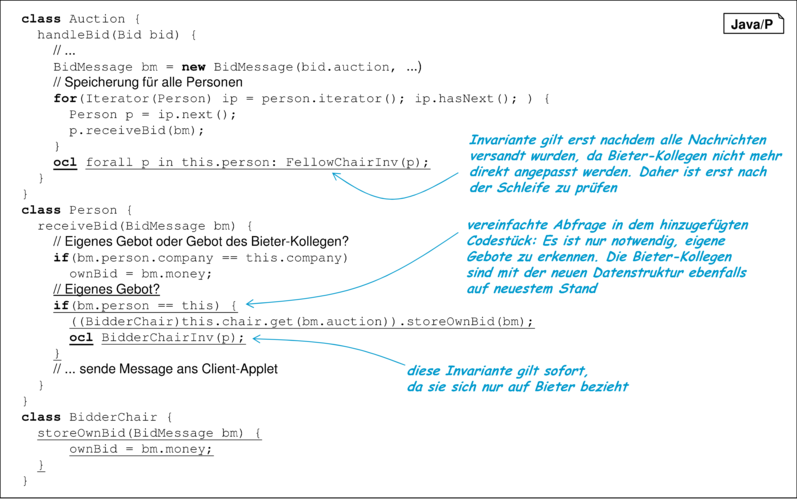
Die Besetzung der neuen Datenstruktur wird in Abbildung 10.19 exemplarisch an der Methode zur Speicherung eines Gebots bei der Person demonstriert. Die Form der hier benutzten Gebote ist bereits in Anhang D, Band 1 beschrieben.
Schritte 5 und 6: Einbau der neuen Datenstruktur/Optimierung
In Kombination mit Schritt 6 erlaubt der Schritt 5 einen stufenweisen Umbau des Systems und dessen Optimierung. Eine konservative Vorgehensweise ist es, zunächst alle bisherigen Methoden weiter anzubieten, um so der Umgebung der modifizierten Datenstruktur die bisherigen Schnittstellen weiterhin zur Verfügung zu stellen. Sinnvoll ist es aber oft auch, zu prüfen, wo Optimierungen zum Beispiel durch Expansion von Methoden günstig sind.
Die konservative Vorgehensweise lässt sich an dem einfachen Beispiel der get- und set-Methoden demonstrieren. In den Abschnitten 4.2.2 und 5.1 ist beschrieben, wie aus einem Attribut des Klassendiagramms bei der Codegenerierung diese get/set-Methoden generiert werden. Wird das Attribut verschoben, so werden die zugehörigen Methoden nicht mehr generiert. Wurden diese Methoden jedoch anderweitig genutzt, so kann eine manuelle Definition dieser Methoden zur Verfügung gestellt werden. Beispielsweise bildet
Java/P  class Person { class Person { |
| Money getOwnBid(Auction a) { |
| return this.chair.get(a).getOwnBid(); |
| }} |
einen geeigneten Ersatz, der auf der neuen Datenstruktur basiert. Die explizite Definition dieser Methode kann auch dazu genutzt werden, die ansonsten standardmäßig generierte Methode zu überschreiben. Deshalb kann mit solchen expliziten Definitionen von get/set-Methoden in sehr einfacher und eleganter Weise der Zugriff von Attributen der alten Datenstruktur auf die neue Datenstruktur umgelenkt werden. Diese konservative Umsetzung ist zunächst geeignet, um die Korrektheit der Umsetzung mit den vorhandenen Tests zu prüfen.
Schritt 7: Entfernung der alten Datenstruktur
Die alte Datenstruktur und mit ihr alle unnötigen Invarianten werden nun entfernt.2
Anpassung der Tests an die neue Datenstruktur
Naturgemäß sind nach einem Refactoring-Schritt nicht mehr alle Tests korrekt. Oft scheitert bereits die Übersetzung eines Tests, weil die aufgerufenen Methoden oder beobachteten Attribute nicht mehr vorhanden sind. Die nach dem Schritt 4 vorhandene doppelte Darstellung der Datenstrukturen kann nun in Schritt 5 genutzt werden, um die vorhandenen Tests zu migrieren. Dabei können Tests, die gegen abstrakte Schnittstellen programmiert wurden unter Umständen ganz ohne oder mit einfachen Transformationen auskommen. Im Gegensatz zum Produktionscode/-modell ist es normalerweise nicht notwendig, für die Optimierung von Tests in Schritt 6 Ressourcen aufzuwenden. Es ist ausreichend die Tests lauffähig und aussagekräftig zu halten. Überflüssige Tests können entfernt werden.
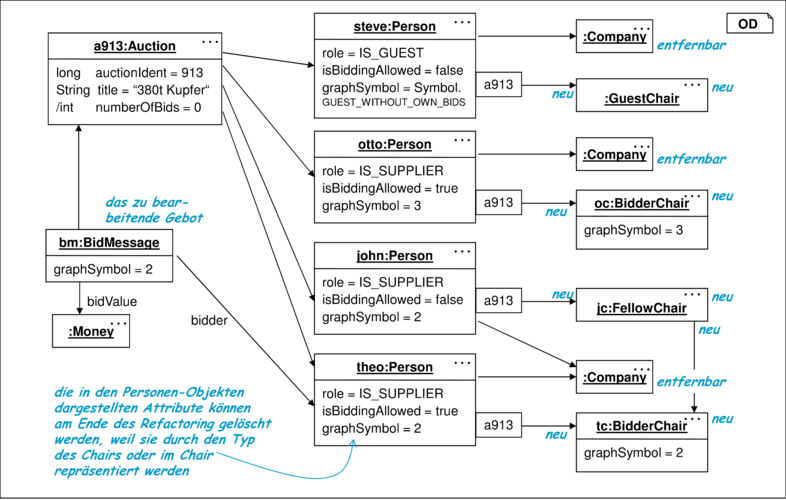
Ein Test besteht aus verschiedenen UML-Diagrammarten. Objektdiagramme werden zum Beispiel für die Darstellung des Testdatensatzes und des Sollergebnisses eingesetzt. Die additive Vorgehensweise führt dazu, dass Objektdiagramme zunächst ebenfalls zu erweitern sind. Das in Abbildung 10.21 dargestelle Objektdiagramm zeigt zum Beispiel einen Ausschnitt eines Testdatensatzes, bei dem bereits die neuen Datenstrukturen hinzugefügt wurden.
Konstruktiv eingesetzte Objektdiagramme müssen eine vollständige Darstellung der Testdaten beinhalten und sind deshalb bei einem Datenstrukturwechsel fast immer betroffen. Demgegenüber erweisen sich als Prädikate eingesetzte Objektdiagramme im additiven Verfahren als relativ stabil, weil sie von dem neu hinzugekommenen Anteil oft nicht betroffen sind.
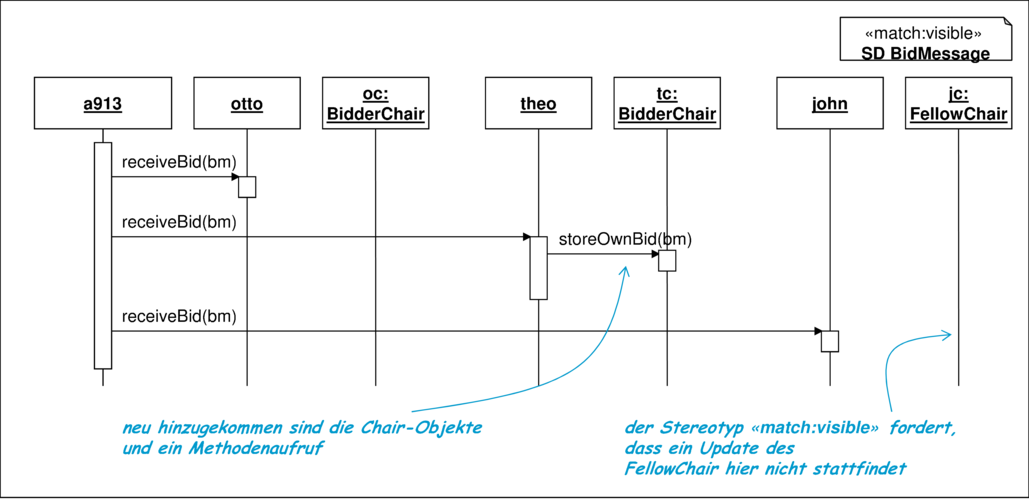
In ganz ähnlicher Weise können Sequenzdiagramme im additiven Verfahren systematisch umgebaut werden. Einem Sequenzdiagramm werden die neuen Interaktionen hinzugefügt, soweit sie von dem dadurch beschriebenen Test beobachtet werden sollen. Wenn eine relativ freie Interpretation der Beobachtung im Sequenzdiagramm zum Beispiel durch den Stereotyp ≪match:free≫ gewählt wurde, dann müssen diese neuen Interaktionen nicht in das Diagramm aufgenommen werden und das Diagramm kann unverändert weiter verwendet werden. Abbildung 10.22 zeigt die Beobachtung der Interaktion von der Auktion mit den beteiligten Personen in Bezug auf die Verteilung der Nachricht für das neue Gebot, in der die Interaktion mit den neuen Chair-Objekten berücksichtigt wird.
Resumee zur additiven Vorgehensweise
Zusammenfassend lässt sich für die hier ausschnittsweise demonstrierten Beispiele und die zugrunde liegende additive Methode zur Durchführung von Refactorings Folgendes feststellen:
- Das Zutrauen in die Korrektheit des Refactorings wird nicht nur durch die vorhandenen, auf der alten Datenstruktur beruhenden Tests, die auf die neue Datenstruktur übertragen werden, hergestellt. Vielmehr werden durch die eingesetzten Invarianten die alte und die neue Datenstruktur in Beziehung gesetzt und dadurch das Zutrauen in die Korrektheit der Transformation weiter erhöht.
- Dem zusätzlichen Aufwand, diese Invarianten zu entwickeln und vorübergehend einzubauen, steht der Vorteil gegenüber, dass durch die additive Vorgehensweise größere Transformationen als Einheit durchführbar werden. Es ist daher nicht notwendig, den im letzten Beispiel durchgeführten Datenstrukturwechsel in eine Anzahl kleinerer Refactoring-Regeln zu zerlegen. Alternativ hätten sonst Einzelschritte ausgeführt werden müssen, um die Klasse Chair zunächst einzuführen, die einzelnen Attribute zu migrieren, die durch Flags dargestellten unterschiedlichen Chair-Varianten durch Unterklassen zu ersetzen und schließlich die Beziehung zwischen FellowChair und BidderChair herzustellen, bevor am Ende die Company-Klasse entfernt werden kann.
- Wie an den Beispielen in den Abbildungen 10.21 und 10.22 illustriert, unterstützt die additive Vorgehensweise auch die Testmigration, indem sie eine Trennung zwischen dem Hinzufügen der neuen und dem Entfernen der alten Datenelemente und Interaktionen in zwei Schritten erlaubt.
Insgesamt qualifiziert sich die additive Methode damit für die Umsetzung von Datenstrukturwechseln als eine effektive Alternative beziehungsweise Ergänzung zu den in [Fow99] beschriebenen Refactoring-Regeln.
Damit können zusätzlich allgemeinere Refactoring-Regeln für UML/P entstehen, die an anderen, ähnlichen Situationen wiederverwendet werden können. Das Prinzip ist hierbei ähnlich wie bei der Entstehung von Frameworks und Entwurfsmustern. Aus einer speziellen Anwendung werden wiederverwendbare Anteile extrahiert und so verallgemeinert, dass dadurch eine allgemeine Regel entsteht. Sonderfälle und alternative Situationen können bei weiteren Anwendungen der Regel erkannt und in die Regel eingearbeitet werden.
Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012
| << zurück | MBSE Home | weiter >> |