Übersicht
Inhaltsverzeichnis
Vorwort
1 Einführung
2 Klassendiagramme
3 Object Constraint Language
3.1 Übersicht über OCL/P
3.2 Die OCL-Logik
3.3 Container-Datenstrukturen
3.4 Funktionen in OCL
3.5 Ausdrucksmächtigkeit der OCL
3.6 Zusammenfassung
4 Objektdiagramme
5 Statecharts
6 Sequenzdiagramme
A Sprachdarstellung durch Syntaxklassendiagramme
B Java
C Die Syntax der UML/P
D Anwendungsbeispiel: Internet-basiertes Auktionssystem
Literatur
| << zurück | MBSE Home | weiter >> |
3.3 Container-Datenstrukturen
In der OCL ist die Navigation über Assoziationen ein wesentliches Konzept zur kompakten Beschreibung von Bedingungen. Ausgehend von einem einzelnen Objekt können durch einen Navigationsausdruck eine Menge oder eine Liste von erreichbaren Objekten beschrieben und ihren Elementen gewisse Eigenschaften zugeordnet werden.
Diese beiden Datenstrukturen dienen zur Verwaltung einer Sammlung von Objekten und werden in der OCL unter dem Oberbegriff Collection zusammengefasst. Im deutschen Sprachgebrauch hat sich dafür eher der Begriff Container durchgesetzt. Die OCL/P bietet in Analogie zu den generischen Typen aus Java drei Typkonstruktoren für Container an. Abbildung 3.7 fasst diese Typkonstruktoren zusammen. Die volle Generizität von Java [Bra04] bietet die OCL allerdings nicht an.
- Set<X>
- beschreibt Mengen über einem Datentyp X. Auf diesen Mengen stehen die üblichen Operatoren wie Vereinigung oder Hinzufügen zur Verfügung. Für den Typ X kann jeder Grunddatentyp, jede Klasse und jeder Containertyp eingesetzt werden. Als Vergleich werden Wertevergleich für Grunddatentypen und die Objektidentität für Klassen verwendet. Allerdings können Objekte ausgewählter Klassen wie zum Beispiel String den Vergleich equals nutzen und überschreiben und damit ebenfalls einen Wertevergleich über ihre Attribute anbieten.
- List<X>
- beschreibt geordnete Listen und die dafür sinnvollen Operationen. List<X> erlaubt die Verwaltung ihrer Objekte in einer linearen Ordnung, beginnend bei dem Index 0.
- Collection<X>
- ist ein Supertyp für die beiden genannten Typen Set<X> und List<X>. Er beinhaltet deren gemeinsame Funktionalität.
Für einen Vergleich von Containern ist eine binäre Operation notwendig, die auf den Elementen einen Test auf Gleichheit durchführt. Sind die Elemente Grunddatentypen oder wieder Container, dann wird für die Elemente der Vergleich == verwendet. Sind die Elemente aber Objekte, so wird der Vergleich equals eingesetzt. Das entspricht einem Wertevergleich für Grunddatentypen und Container7 sowie normalerweise einem Vergleich der Objektidentität auf Objekten. Für spezielle Typen, wie zum Beispiel Strings, wird jedoch equals überschrieben und damit ein Wertevergleich angeboten.8
Die Subtypbeziehung von Set<X> und List<X> zu Collection<X> erlaubt es, für jeden beliebigen Typ X statt Werten des Typs Collection<X> Werte der Typen Set<X> oder List<X> einzusetzen.
Container können in komplexere Typstrukturen geschachtelt werden. So sind zum Beispiel folgende Datentypen in der OCL/P erlaubt:
inv:
let Set<int> si = { 1, 3, 5};
Set<Set<int>> ssi = { {}, {1}, {1,2}, si };
Set<Set<int>> lsp = List{ {1}, {} }
in ...
Bei einem Typkonstruktor Set<X> ist also für den Elementtyp X ist ein beliebiger Datentyp einsetzbar. Die Erfahrung zeigt allerdings, dass verschachtelte Datenstrukturen die Komplexität eines Modells stark erhöhen und deshalb nur sehr eingeschränkt verwendet werden sollten. Diese Komplexität kann beispielsweise durch die Einbettung komplexer Datenstrukturen in eigens dafür entworfene Klassen abgeschottet werden. In der OCL/P werden verschachtelte Containerstrukturen vermieden, indem die Navigation entlang von Assoziationen nur flachgedrückte Containerstrukturen als Ergebnisse hat. Siehe dazu Abschnitt 3.3.8.
Die OCL/P weist einige Unterschiede zum OCL-Standard in Bezug auf Container auf. So wurde der aus Java übernommene Typkonstruktor List anstatt Sequence eingeführt. Außerdem wurde auf einen Typkonstruktor für Multimengen verzichtet. Dies geschah aus rein pragmatischen Gründen, denn in der Praxis hat sich gezeigt, dass Multimengen ein selten gebrauchtes und eher zur Komplexitätssteigerung beitragendes Konzept sind.
3.3.1 Darstellung von Mengen und Listen
Eine Klasse (beziehungsweise ein Interface) kann in der OCL gleichzeitig als Typ und als Extension, also die Menge aller aktuell existierenden Objekte, verwendet werden. Beispielsweise beschreibt
inv:
Auction.size < 1700
die maximale Anzahl von gleichzeitigen Auktionen im System. Der Ausdruck Auction bezeichnet damit die Menge aller aktuell existenten Objekte des Typs Auction. Diese Menge hat den Typ Set<Auction>. In ihr enthalten sind alle Objekte, die zur Klasse Auction oder einer Unterklasse gehören. Zur Bildung einer Extension dürfen nur objektwertige Klassen und Interfaces verwendet werden. Weder Grunddatentypen, noch Container-Typen stellen Extensionen dar.
Eine zweite Möglichkeit zur Beschreibung von Mengen ist die direkte Aufzählung in der Form Set{...} mit einer durch Kommata getrennten Liste von Objekt-Ausdrücken. Beispielsweise ist Set{} die leere Menge, Set{8,5,6,8} eine Menge aus drei ganzen Zahlen und Set{"text", (Auction)a} eine aus einem String und einem Auktions-Objekt bestehende Menge. Optional kann der Indikator Set auch weggelassen werden, denn {}, {8,5,6,8} und {"text",(Auction)a} beschreiben die gleichen Mengen.
Wie das letzte Beispiel zeigt, ist bei einer Aufzählung von Mengen mit heterogenen (also unterschiedlich typisierten) Argumenten Typkorrektheit sicher zu stellen. Dazu wird festgelegt, dass der Typ des ersten Arguments X den Typ des Gesamtausdrucks Set<X> bestimmt. Alle weiteren Argumente der Liste müssen typkompatibel zu X sein. Bei homogenen Aufzählungen gleichen Typs ist das unkritisch, bei heterogenen Aufzählungen kann der gewünschte Ergebnistyp durch eine explizite Nennung des Typs erzwungen werden: Set<Object>{"text",(Auction)a} wird mit Set<Object> typisiert. Auch die leere Menge kann entsprechend typisiert werden, z.B. als Set<Person>{}. Ist kein Typ angegeben, so wird der Elementartyp offen gelassen, also eine anonyme Typvariable angenommen.
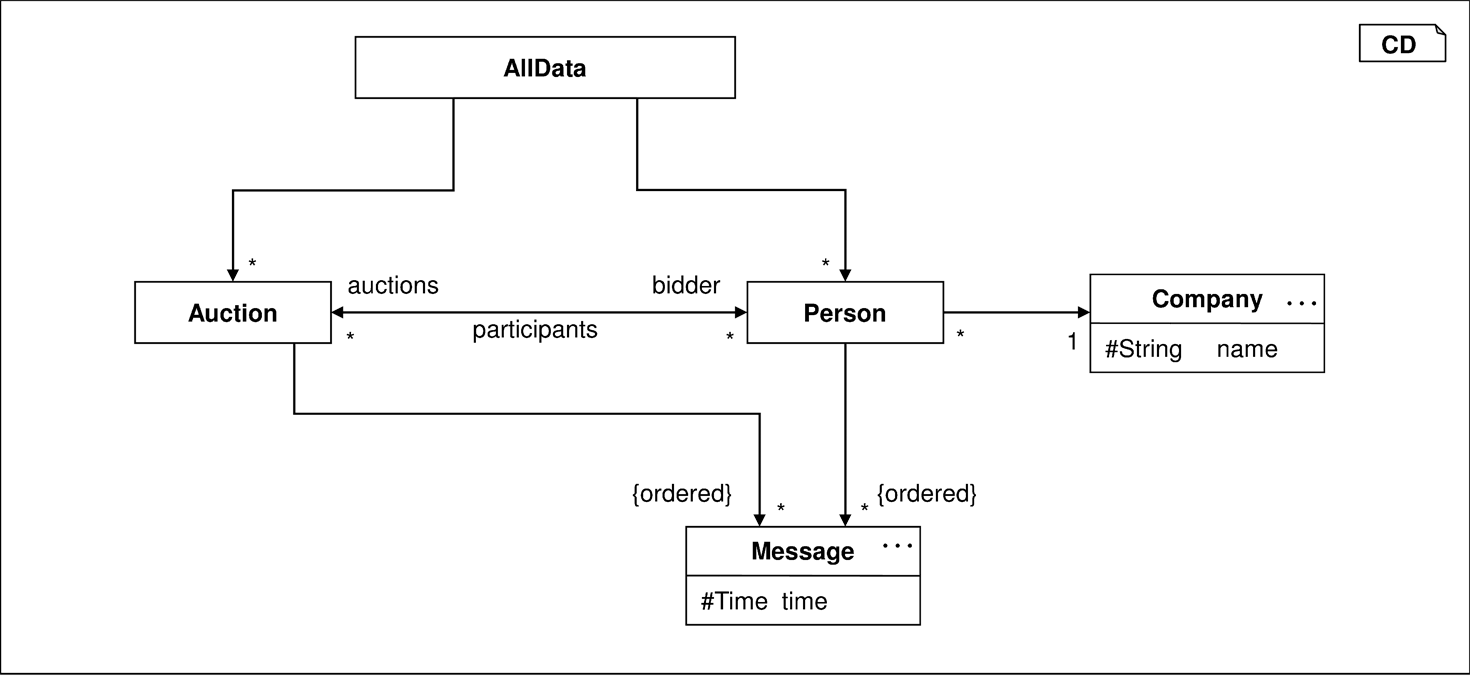
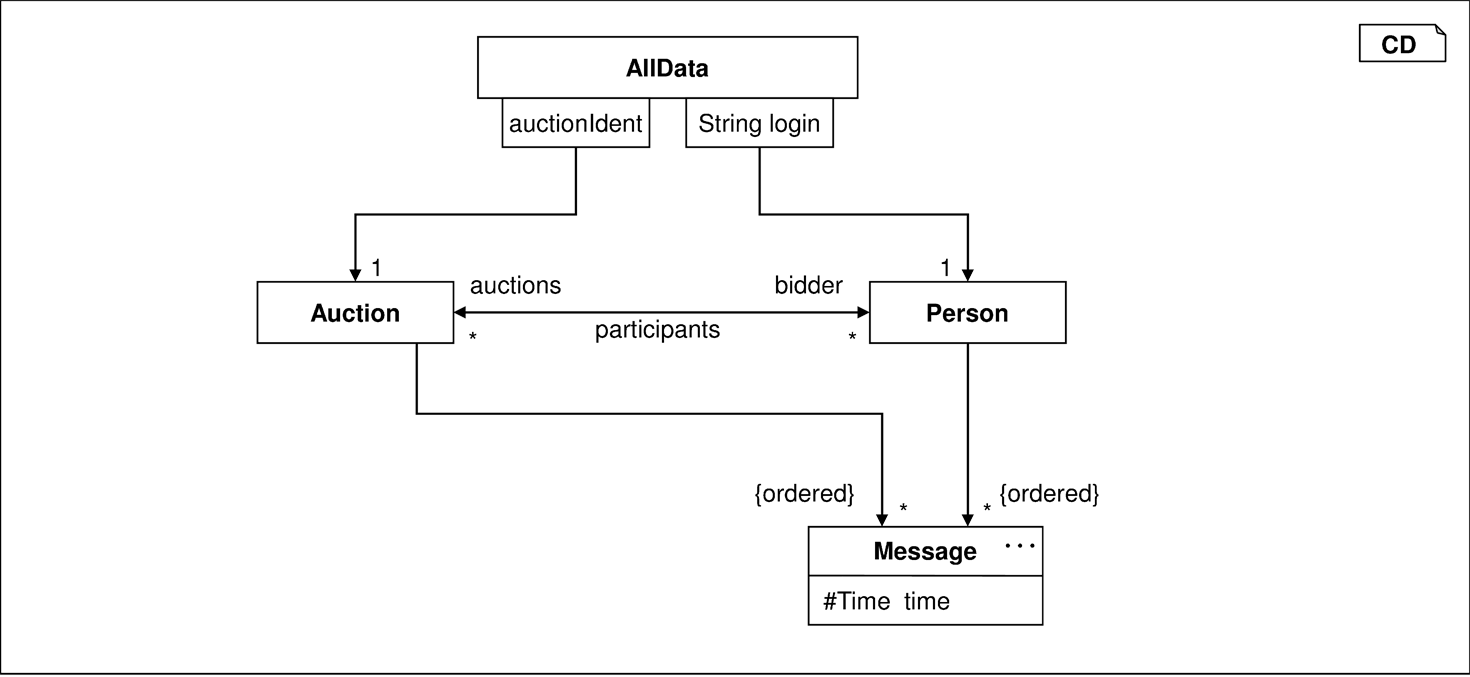
Der Ausschnitt des Auktionssystems in Abbildung 3.8 dient als Grundlage für weitere OCL-Beispiele. Nachfolgende Bedingung beschreibt unter Benutzung der Extension der Klasse AllData und einer einelementigen Menge, dass die Klasse AllData genau ein Objekt instanziiert, also ein Singleton [GHJV94] darstellt:
context AllData ad inv AllDataIsSingleton:
AllData == {ad}
3.3.2 Mengen- und Listenkomprehension
OCL/P bietet gegenüber dem OCL-Standard eine reichhaltige Sammlung von Möglichkeiten zur eigenschaftsorientierten und zur aufzählenden Beschreibung von Mengen und Listen. Diese wurden aus der funktionalen Programmiersprache Haskell [Hut07] übernommen. Sie erlauben einen kompakten Umgang mit Containern und haben eine präzise und elegante Bedeutung. Da für Mengen generell die folgende Umwandlung für einen korrekten Rumpf „characterization“ gilt, wird die Beschreibung für Listen erklärt.9
Set{ characterization } == List{ characterization }.asSet
Aufzählungen von Listen ganzer Zahlen und von Zeichen können mittels List{n..m} beschrieben werden. Beispiele sind:
inv:
List{-3..3} == List{-3,-2,-1,0,1,2,3};
List{1..1} == List{1};
List{9..5} == List{};
List{1,3..9} == List{1,3,5,7,9};
List{9,8..5} == List{9,8,7,6,5};
List{'a'..'c'} == List{'a','b','c'};
List{3..5,7..9} == List{3,4,5,7,8,9};
List{3..(2+5)} == List{3,4,5,6,7};
Bei einer Aufzählung wird also sowohl das erste als auch das letzte Element in der Liste aufgenommen. Listen können Schrittweiten nutzen. Aufzählungen und einzelne Elemente können gemischt angegeben werden. Die angegebenen Grenzen müssen auch keine Konstanten sein.
Während Aufzählungen nur für die Aufzählungstypen Zahlen und Buchstaben geeignet sind, können Listenkomprehensionen viel allgemeiner eingesetzt werden. Die generelle Syntax einer Listenkomprehension ist von der Form:
List{ expr | characterization }
Dabei werden in der Charakterisierung (rechts) neue Variablen definiert, die in dem Ausdruck (links) genutzt werden können. Die Charakterisierung besteht deshalb aus mehreren, durch Kommata getrennten Variablendefinitionen und einschränkenden Bedingungen. Die Beschreibungsmächtigkeit der Listenkomprehension besteht gerade in der Kombination der nachfolgend vorgestellten drei Mechanismen: dem Generator, dem Filter und der lokalen Variablendefinition.
Ein Generator v in list lässt eine neue Variable vüber eine Liste list variieren. Beispielsweise können so Quadratzahlen beschrieben werden:
inv:
List { x*x | x in List{1..5} } == List{1,4,9,16,25}
Der Typ der Variable x ist gleich dem Elementtyp der Liste, über der variiert wird. Er kann aber auch wie bei anderen lokalen Variablendefinitionen explizit angegeben werden. Im folgenden Beispiel werden Nachrichten in Millisekunden umgerechnet:
context Auction a inv:
let List<long> tlist =
List{ m.time.asMsec() | Message m in a.message }
in ...
Der Filter beschreibt eine Einschränkung auf einer Liste von Elementen. Ein solcher Filter evaluiert zu einem Wahrheitswert, der darüber entscheidet, ob ein Element in einer Liste aufgenommen ist. In seiner reinen Form ohne Kombination mit einem Generator ist seine Charakterisierung:
List{ expr | condition } ==
if condition then List{ expr } else List{}
In Kombination mit einem Generator können so Filter für Teillisten beschrieben werden. Zum Beispiel kann eine Liste ungerader Quadratzahlen mit10
inv:
List { x*x | x in List{1..8}, !even(x) } == List{1,9,25,49}
beschrieben werden. Analog kann eine Liste von Nachrichten nach Zeiträumen gefiltert werden:
context Auction a inv MessageTimes:
let List<long> tlist = List{ m.time.asMsec()
| m in a.message, m.time.lessThan(a.startTime) }
in ...
Zur weiteren Unterstützung des Beschreibungskomforts können Zwischenergebnisse berechnet und lokalen Variablen zugewiesen werden. Die Definition einer neuen Variable hat die Form v=Ausdruck und ist wie die Einführung einer neuen Variable mittels let-Konstrukt zu verstehen. Der Typ der Variable kann explizit angegeben werden, oder er wird wie bei dem let-Konstrukt aus dem Typ des Ausdrucks inferiert. Die Menge aller ungeraden Quadratzahlen kann damit auch so beschrieben werden:
inv:
List { y | x in List{1..8}, int y = x*x, !even(x) } ==
List{1,9,25,49}
Die Definition MessageTimes kann damit modifiziert werden zu:
context Auction a inv MessageTimes2:
let List<long> tlist = List{ t | m in a.message,
t = m.time.asMsec(), t < a.startTime.asMsec() }
in ...
Dieses Beispiel zeigt auch, wie hilfreich die Kombination der Filter, Generatoren und Variablendefinitionen ist. Nützlich ist auch die Verwendung mehrerer Generatoren, wie beispielsweise die Generierung von konkatenierten Strings zeigt:
inv:
List { z+"?" | x in List{"Spiel","Feuer","Flug"},
y in List{"zeug","platz"},
String z = x+y,
z != "Feuerplatz" }
==
List {"Spielzeug?", "Spielplatz?",
"Feuerzeug?",
"Flugzeug?", "Flugplatz?" }
Dabei ist die Reihenfolge der entstehenden Liste präzise festgelegt. Die Generatoren werden von rechts nach links variiert. Zunächst werden also alle Elemente des rechten Generators durchlaufen. Auch dürfen die weiter rechts stehenden Charakterisierungen, meistens Bedingungen, auf die Variablen der links stehenden Charakterisierungen, also Generatoren und lokale Definitionen, zugreifen.
Bei Generatoren wurden bisher immer listenwertige Datentypen vorausgesetzt. Ein Generator kann aber auch mengenwertig sein und dennoch in der Listenkomprehension eingesetzt werden. Jedoch ist die Reihenfolge der Liste für den Anwender nicht eindeutig:
inv:
let la = List{ a | a in Set{1,2} }
in la == List{1,2} || la == List{2,1}
Die fehlende Eindeutigkeit dieser Beschreibung hat für eine Realisierung den Vorteil, dass Freiheitsgrade erhalten bleiben. Wesentlich ist aber, dass trotz der dem Anwender gegenüber nicht eindeutigen Beschreibung des Ergebnisses, das Ergebnis determiniert ist. Das heißt, derselbe OCL-Ausdruck hat in demselben Kontext immer denselben Wert. Insbesondere gilt nach dieser Konvention:
inv:
let la = List{ a | a in Set{1,2} };
lb = List{ a | a in Set{1,2} }
in la == lb
Bei Benutzung einer Menge als Generator in einer Listenkomprehension wird implizit eine Konvertierung mittels asList durchgeführt. Folgende Eigenschaft kann daher als charakterisierend angenommen werden:
inv:
List{ a | a in Set{1,2} } ==
Set{ a | a in Set{1,2} }.asList
Im umgekehrten Fall werden auch Listengeneratoren in Mengen konvertiert. Diese Umsetzung ist allerdings eindeutig.
Weil in OCL jede Klasse gleichzeitig seine Extension darstellt, kann auf besonders einfache Weise auf alle Objekte einer Klasse zugegriffen werden. Die Menge aller laufenden oder abgeschlossenen Auktionen kann deshalb beschrieben werden durch:
inv:
let Set<Auction> sa =
Set{ a | a in Auction, Time.now().lessThan(a.startTime) }
in ...
Da die Kombination eines Generators a in Auction mit einem Filter besonders häufig vorkommt, gibt es dafür eine Kurzform, bei der der erste Generator bereits links angegeben werden kann:
inv:
let Set<Auction> sa =
Set{ a in Auction, Time.now().lessThan(a.startTime) }
in ...
3.3.3 Mengenoperationen
Die für Mengen zur Verfügung stehenden Operationen sind in Abbildung 3.9 aufgelistet. Diese Signatur stellt eine Integration der aus der Java-Realisierung von Mengen bekannten und der vom OCL-Standard angebotenen Funktionalität dar und ist als Sammlung von Methodensignaturen wiedergegeben. Bei sich widersprechenden Namen der Operatoren mit gleicher Funktionalität wurden die Java-Namen gewählt. Die Operationen size, isEmpty und asList können in OCL wie Attribute ohne Klammern geschrieben werden, denn eine Query ohne Argumente kann grundsätzlich wie ein Attribut behandelt werden. Eine Schreibweise als Query mit Klammern ist wegen der Kompatibilität zu Java ebenfalls möglich.
| Set<X> add(X o); |
| Set<X> addAll(Collection<X> c); |
| boolean contains(X o); |
| boolean containsAll(Collection<X> c); |
| int count(X o); |
| boolean isEmpty; |
| Set<X> remove(X o); |
| Set<X> removeAll(Collection<X> c); |
| Set<X> retainAll(Collection<X> c); |
| Set<X> symmetricDifference(Set<X> s); |
| int size; |
| X flatten; // NB: nur für Collection-Typ X |
| List<X> asList; |
Mit Ausnahme des flatten-Operators, der in Abschnitt 3.3.6 diskutiert wird, sind die Mengenoperatoren analog zu Java und benötigen keine detaillierte Beschreibung. Deshalb sollen hier nur einige wesentliche Punkte herausgegriffen werden.
Im Gegensatz zu einer Java-Implementierung ist für OCL-Ausdrücke das Konzept der Exceptions nicht vorhanden. Stattdessen sind alle Operatoren der OCL robust in dem Sinne, dass ihre Interpretation immer sinnvolle Ergebnisse ergibt. Zum Beispiel hat der Ausdruck Set{e}.add(e) als Ergebnis Set{e}.
Gleichheit auf Mengen und Elementen
In Java gibt es die Gleichheit auf Identifikatoren == und die für jede Klasse individuell definierbare Gleichheitsoperation equals. Letztere wird innerhalb von Java-Containern für den Vergleich von Elementen verwendet und erlaubt damit eine Flexibilisierung des Elementvergleichs in der Implementierung. Diese Unterscheidung existiert auch in einigen Spezifikationssprachen [BFG+93], die neben einer eingebauten eine frei definierbare Gleichheit erlauben. Weil in der OCL Container keine Objektidentität besitzen, sind auf Containern beide Operatoren == und equals identisch:
context Set<X> sa, Set<X> sb inv:
sa.equals(sb) <=> sa == sb
Nach Definition gilt die Gleichheit zweier Mengen genau dann, wenn beide paarweise gleiche Elemente haben. Dabei wird bei dem Vergleich der Elemente equals für Objekte und == für Grunddatentypen verwendet. Ist X also ein Grunddatentyp oder Container, so gilt:
context Set<X> sa, Set<X> sb inv:
sa == sb <=> (forall a in sa: exists b in sb: a == b) &&
(forall b in sb: exists a in sa: a == b)
Für Objekttypen X gilt:
context Set<X> sa, Set<X> sb inv:
sa == sb <=> (forall a in sa: exists b in sb: a.equals(b)) &&
(forall b in sb: exists a in sa: a.equals(b))
Damit ist in der OCL == für Container von der frei definierbaren Gleichheit equals auf den Elementen abhängig und unterscheidet sich von dem Vergleich in Java.
Typinferenz bei heterogenen Mengen
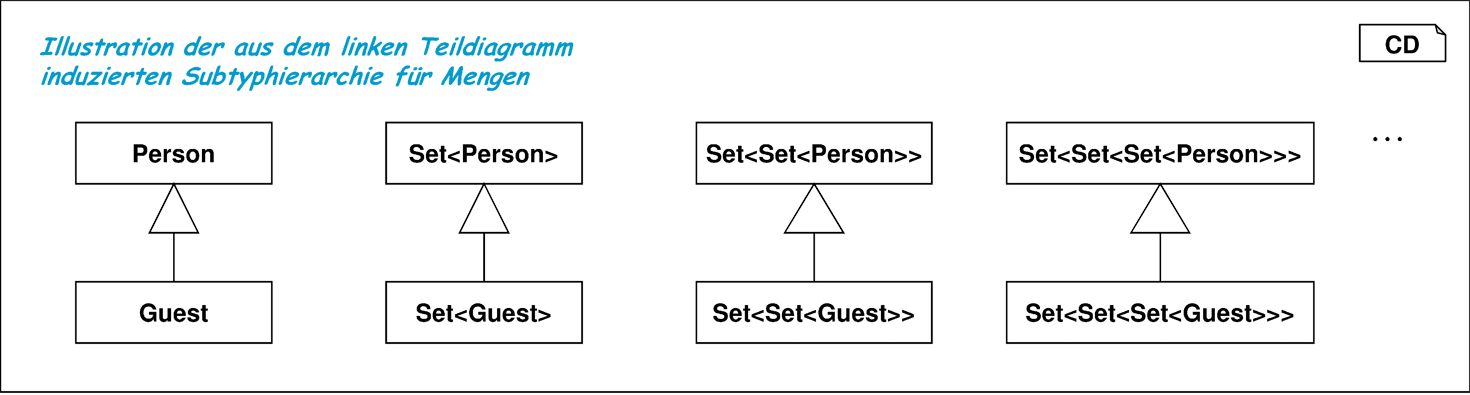
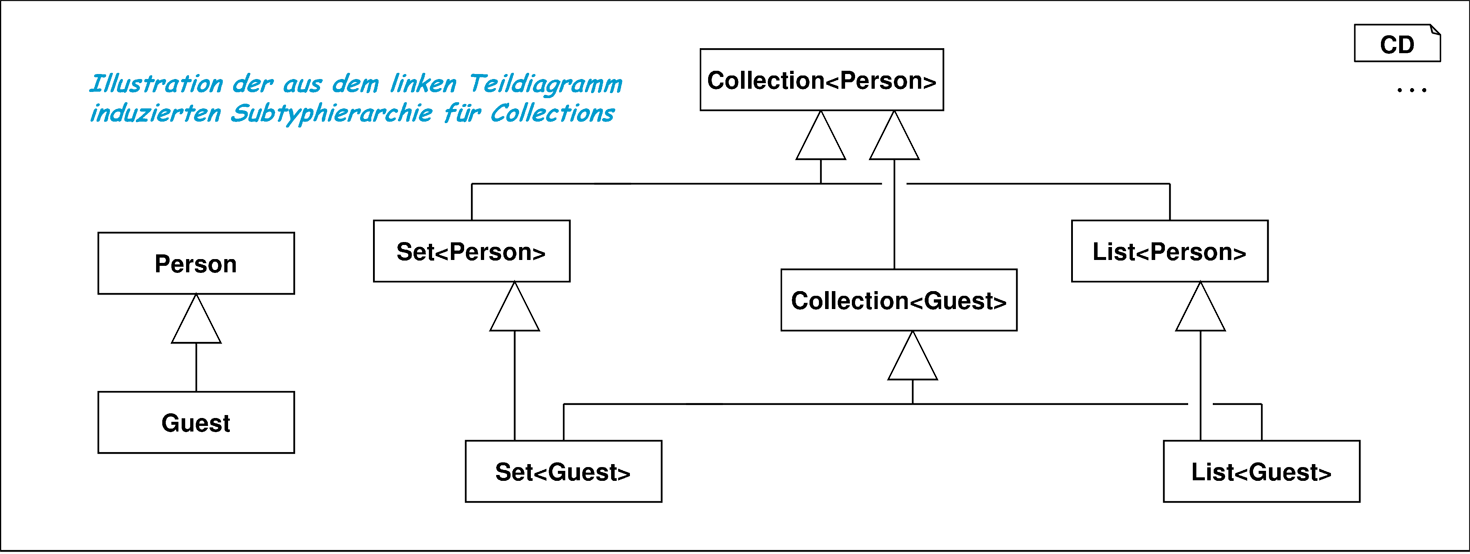
Eine Feinheit der OCL ist die automatische Typkonversion von Argumenten der Mengenoperatoren. Ist Guest eine Unterklasse von Person, so zeigt Abbildung 3.10 einen Teil der daraus induzierten Subtyphierarchie für Container. Hier unterscheidet sich die OCL vom Typsystem in Java [GJSB05], die eine Subtypbeziehung zwischen Set<Guest> und Set<Person> nicht zulassen kann, weil in Java Sets als modifizierbare, identitätsbehaftete Objekte realisiert sind und man sonst Person-Objekte in Set<Guest>-Mengen vornehmen könnte. In der OCL besitzen Container grundsätzlich keine Identität. Im strengen Sinne werden sie auch nicht modifiziert, sondern z.B. beim Hinzufügen immer neue Container erzeugt, kann hier die Subtypbeziehung etabliert werden.
Das bedeutet insbesondere, dass die Vereinigung einer Menge von Personen mit einer Liste von Gästen möglich ist, da letztere implizit zum Typ Collection<Person> konvertiert werden kann. Das Ergebnis dieser Vereinigung (mit Funktion addAll) ist gemäß der Signatur in Abbildung 3.9 wieder eine Menge von Personen:
let Set<Person> pset = ...;
List<Guest> glist = ...
in
pset.addAll(glist) // hat den Typ Set<Person>
Bei heterogener Nutzung von Mengenoperatoren werden also gegebenenfalls die Typen von Argumenten konvertiert. Die Menge, auf die der Operator angewandt wird, wird allerdings nicht konvertiert. In folgender Bedingung ist deshalb die letzte Zeile nicht typkorrekt:
let Set<Person> pset = ...;
Set<Guest> gset = ...
in
gset.addAll(pset) // nicht typkorrekt
In [Sch02] wird darauf hingewiesen, dass die Typisierungsregeln für OCL verallgemeinert werden können, um dem letzten Ausdruck einen korrekten Typ zuzuweisen. Im Prinzip könnten aus dem Wissen über das Ergebnis einer Operation sogar weitere Typinformationen gewonnen werden. So beinhaltet der folgende Schnitt zweier Mengen:
let Set<Person> pset = ...;
Set<Guest> gset = ...
in
pset.retainAll(gset)
nur Objekte der Klasse Guest und könnte damit nicht nur den vom Typsystem berechneten Typ Set<Person>, sondern sogar den Subtyp Set<Guest> haben.
Allerdings ist in der Anwesenheit von Mehrfachvererbung beziehungsweise mehrfacher Instanziierbarkeit von Interfaces wie in Java eine eindeutige Zuweisung eines Typs nicht immer möglich. Auch kann die restriktivere Typisierung für das erste Argument hier als Schutz verstanden werden, die den Modellierer zwingt, gegebenenfalls eine explizite Typkonversion des ersten Arguments vorzunehmen.
3.3.4 Listenoperationen
Auch für Listen existieren eine Reihe von Operationen zur Selektion, Kombination und Bearbeitung. Genau wie bei Mengen ist die Interpretation von Container-Ausdrücken frei von Seiteneffekten und unterscheidet sich damit von den in Java angebotenen Listen.
Die Listenoperationen sind in Abbildung 3.11 wiedergegeben. Wie bei Mengen (siehe Abbildung 3.9) wurde auch hier eine Integration der aus der Java-Realisierung von Listen bekannten und der vom OCL-Standard angebotenen Funktionalität vorgenommen.
| List<X> add(X o); |
| List<X> add(int index, X o); |
| List<X> prepend(X o); |
| List<X> addAll(Collection<X> c); |
| List<X> addAll(int index, Collection<X> c); |
| boolean contains(X o); |
| boolean containsAll(Collection<X> c); |
| X get(int index); |
| X first; |
| X last; |
| List<X> rest; |
| int indexOf(X o); |
| int lastIndexOf(X o); |
| boolean isEmpty; |
| int count(X o); |
| List<X> remove(X o); |
| List<X> removeAtIndex(int index); |
| List<X> removeAll(Collection<X> c); |
| List<X> retainAll(Collection<X> c); |
| List<X> set(int index, X o); |
| int size; |
| List<X> subList(int fromIndex, int toIndex); |
| List<Y> flatten; // NB: X hat die Form Collection<Y> |
| Set<X> asSet; |
Für praktische Belange ist es angenehm, da systematischer, die aus Java bekannte Indizierung der Listenelemente mit 0 zu beginnen und die hintere Grenze bei subList auszuschließen. Die Eigenschaften der Listen sollen an einigen gültigen Aussagen demonstriert werden:
List{0,1} != List{1,0};
List{0,1,1} != List{0,1};
List{0,1,2}.add(3) == List{0,1,2,3};
List{'a','b','c'}.add(1,'d') == List{'a','d','b','c'};
List{0,1,2}.prepend(3) == List{3,0,1,2};
List{0,1}.addAll(List{2,3}) == List{0,1,2,3};
List{0,1,2}.set(1,3) == List{0,3,2};
List{0,1,2}.get(1) == 1;
List{0,1,2}.first == 0;
List{0,1,2}.last == 2;
List{0,1,2}.rest == List{1,2};
List{0,1,2,1}.remove(1) == List{0,2};
List{0,1,2,3}.removeAtIndex(1) == List{0,2,3};
List{0,1,2,3,2,1}.removeAll(List{1,2}) == List{0,3};
List{0..4}.subList(1,3) == List{1,2};
List{0..4}.subList(3,3) == List{};
Das Hinzufügen der Elemente eines Containers zu einer Liste mittels addAll hat nur dann ein eindeutiges Ergebnis, wenn dieser Container selbst eine Liste ist. Andernfalls liegt die Reihenfolge der neu hinzugefügten Elemente nicht fest. Dennoch ist nach Konvention gesichert, dass ein OCL-Ausdruck determiniert ist, also derselbe OCL-Ausdruck in dem selben Kontext immer gleiche Werte beschreibt. Insbesondere gilt:
inv:
forall s1 in Set<X>, s2 in Set<X>:
s1 == implies s1.asList == s2.asList
Die Operationen remove und removeAll entfernen jeweils alle Auftreten ihrer Argumente in der bearbeiteten Liste. Als Vergleich wird dabei die Gleichheit equals für Objekte und == für Basisdatentypen verwendet. Anders als in Java kann das Entfernen eines Elements an einem bestimmten Index nicht ebenfalls remove heißen, da Listen direkt mit Elementen von Grunddatentypen, also auch mit int besetzt sein können. Deshalb wurde dafür removeAtIndex eingeführt.
3.3.5 Container-Operationen
Ein Container ist entweder eine Menge oder eine Liste. Deshalb wird auch den Containern eine Signatur zugewiesen, die aus allen auf Mengen und Listen gemeinsamen Operationen besteht. In Abbildung 3.12 ist die Signatur für Container zusammengefasst.
| Collection<X> add(X o); |
| Collection<X> addAll(Collection<X> c); |
| boolean contains(X o); |
| boolean containsAll(Collection<X> c); |
| boolean isEmpty; |
| int count(X o); |
| Collection<X> remove(X o); |
| Collection<X> removeAll(Collection<X> c); |
| Collection<X> retainAll(Collection<X> c); |
| int size; |
| Collection<Y> flatten; // NB: X hat die Form Collection<Y> oder Set<Y> |
| List<Y> flatten; // NB: X hat die Form List<Y> |
| Set<X> asSet; |
| List<X> asList; |
Die Konversionsfunktionen asSet und asList erlauben es, beliebige Container in Mengen beziehungsweise Listen zu wandeln. Bei Anwendung einer dieser Operationen findet eine echte Umwandlung statt. Demgegenüber hat eine Typkonversion mittels (Set<X>) oder (List<X>) sowie auch mittels (Collection<X>) den Sinn, Typinformation zu verändern, ohne die zugrunde liegende Datenstruktur zu modifizieren. Deshalb ist für eine Liste l die Umwandlung in eine Menge l.asSet sinnvoll, die Typkonversion (Set<X>)l aber verboten. Das Zusammenspiel dieser Konversionen lässt sich durch folgende Beispiele illustrieren:
let Collection<int> ci List{1,2,1};
in
ci.asSet == {1,2} &&
ci.asList == List{1,2,1} &&
ci.asSet.asList.size == 2 &&
(List<int>) ci == List{1,2,1} &&
!( (Set<int>) ci == {1,2} ) && // da linke Seite undefiniert
In Kombination mit dem typeif-Operator kann eine sichere Typkonversion vorgenommen werden, die eine explizite Typkonversion und die damit verbundenen Fehlermöglichkeiten verhindert und den Spezifikateur dazu bringt, über den Fall einer fehlerhaften Typkonversion explizit nachzudenken. Soll zum Beispiel aus obiger Liste ci mit dem Typ Collection<int> das zweite Element selektiert werden, so kann dies wie folgt aussehen (-42 ist ein gewählter Ersatzwert):
let Collection<int> ci List{1,2,1};
in result ==
typeif ci instanceof List<int> then ci.get(0) else -42
Der obige Ausdruck stellt eine Kurzform dar für
let Collection<int> ci List{1,2,1};
in result ==
if ci instanceof List<int> then
let List<int> cinew = (List<int>) ci
in cinew.get(0)
else -42
Dabei wird die Hilfsvariable cinew nur benötigt, um dem in ci gespeicherten Wert einen anderen Typ zuzuweisen, der den Zugriff als Listenelement erlaubt.
3.3.6 Flachdrücken von Containern
Tief geschachtelte Container-Strukturen enthalten eine gewisse Strukturierungsinformation, die in manchen Fällen zur Spezifikation von Systemen hilfreich ist. So kann mit dem Typ Set<Set<Person>> eine Gruppierung von Personen beschrieben werden.
let Set<Set<Person>> ssp = { a.bidder | a in Auction }
beschreibt die Gruppen von Personen, die jeweils an einer Auktion teilnehmen.
Oft ist jedoch diese tiefe Strukturierung nicht erwünscht und eine einfache Menge beziehungsweise Liste reicht bereits aus. Der Operator flatten wird deshalb dazu verwendet, geschachtelte Container-Strukturen flach zu drücken.
Die in den Abbildungen 3.9, 3.11 und 3.12 angegebenen Nebenbedingungen für diesen Operator zeigen, dass er nur auf geschachtelte Container-Strukturen angewandt werden darf. In Abhängigkeit der Art der Container entsteht beim Flachdrücken entweder eine Menge oder eine Liste. Wenn von dem Argument allerdings nur der Typ Collection bekannt ist, so ist gegebenenfalls über das Ergebnis wieder nur bekannt, dass es eine Collection ist. Die verschiedenen Ausprägungen des flatten-Operators haben die in Abbildung 3.13 angegebenen Signaturen, wobei links das Ergebnis und vor dem Punkt der Typ des Arguments angegeben ist.
| Set<X> Set<Set<X>>.flatten; |
| List<X> Set<List<X>>.flatten; |
| Collection<X> Set<Collection<X>>.flatten; |
| List<X> List<Set<X>>.flatten; |
| List<X> List<List<X>>.flatten; |
| List<X> List<Collection<X>>.flatten; |
| Collection<X> Collection<Set<X>>.flatten; |
| List<X> Collection<List<X>>.flatten; |
| Collection<X> Collection<Collection<X>>.flatten; |
Der flatten-Operator verschmilzt nur die beiden „oberen“ Ebenen von Containern, ohne sich um die interne Struktur des darin enthaltenen Elementtyps X zu kümmern. Man spricht auch von schmalem (engl.: shallow) Flachdrücken. Ein vollständiges Flachdrücken zu einer Menge oder Liste einfacher Objekte kann durch mehrfache Anwendung erreicht werden.
Generell wurde beim Flachdrücken von Containern der Grundsatz angewandt, dass eine Liste entsteht, wenn eine Liste beteiligt ist (Listen also dominieren). Ist keine Liste, aber ein Container beteiligt, so entsteht ein Container. Nur verschachtelte Mengen werden wieder zu Mengen.11
Abbildung 3.14 zeigt exemplarisch einige Anwendungen des flatten-Operators.
Die Benutzung verschachtelter Container führt teilweise zu komplexer formulierten Bedingungen, als es die Problemstellung erfordert. Deshalb wird der flatten-Operator bei Navigationsketten implizit eingesetzt, so dass das Ergebnis einer Navigationskette nie eine Container-Struktur darstellt, die tiefer verschachtelt ist als die Ausgangsstruktur. Einzige Ausnahme bildet die Navigationskette ausgehend von einem einzelnen Objekt, die zu einer Menge oder Sequenz führen kann.
3.3.7 Typisierung von Containern
In den vorherigen Abschnitten wurde bereits vereinzelt die Problematik der korrekten Typisierung von OCL-Ausdrücken diskutiert. Dieser Abschnitt enthält nun eine Übersicht, in der die bereits diskutierten Aspekte kurz wiederholt werden:
- Es gibt eine aus Java bekannte Sammlung von Grunddatentypen. Subtypen existieren nur zwischen Zahlen in der bekannten Form.
- Jede Klasse und jedes Interface des der OCL zugrunde liegenden Modells ist ein Typ. Dabei sind insbesondere Klassen der Java-Bibliotheken und alle Typinstanziierungen generischer Klassen eingeschlossen. Die Vererbungsbeziehungen aus dem Klassendiagramm werden übernommen. Der besondere Typ Objekt ist die gemeinsame Oberklasse aller dieser Typen (Grunddatentypen und Container ausgeschlossen).
- Durch Verwendung der Typkonstruktoren werden mengen- und listenwertige Typen sowie Typen für Abbildungen aufgebaut. Für alle Typen X sind Set<X>, List<X> und Collection<X> wieder Typen.
- Bei Operationen mit mehreren gleich typisierten Argumenten und einem Container als Ergebnis wird normalerweise das erste Argument herangezogen, um den Elementtyp des Containers zu bestimmen. Dazu zählen auch Aufzählungen. Gegebenenfalls ist das erste Argument geeignet zu typisieren. Beispiel: Set{(Object)"Text", person}.
Abbildung 3.10 zeigt, wie sich die Subtyphierarchie von Klassen auf die entsprechenden Container-Typen auswirkt. Da Container-Typen beliebig schachtelbar sind, werden wie in Abbildung 3.15 illustriert, dadurch weitere Typen und Subtypbeziehungen induziert.
Die Klasse Object ist in Java, genauso wie in der OCL/P, die allgemeinste Oberklasse, die alle anderen Klassen und Interfaces enthält. Das bedeutet, dass die Extension von Object alle Objekte des Systems beinhaltet. Im Gegensatz zu Java sind Container in der OCL keine Klassen. Deshalb gilt keine Vererbungsbeziehung zwischen Set<Person> und Object. Durch die strikte Trennung der Typhierarchie für Objekte und Mengen von Objekten werden einige semantisch unangenehme Implikationen verhindert. So ist etwa Set<Object> kein Subtyp von Object und es ist durch die Typisierung gesichert, dass eine Menge nicht sich selbst als Element enthalten kann12 . Diese Trennung pflanzt sich auf weitere Ebenen fort. So ist beispielsweise Set<Set<Object>> in keiner Subtypbeziehung mit Set<Object>, und List<Object> nicht mit Object.
Deshalb ist die Bildung folgender Menge, die die Anomalie der Mengentheorie veranschaulicht, nicht typkorrekt13 :
let Set<Object> x =
{ Object y | yinstanceof Set<Object>
&& !(y in (Set<Object>)y) }
in ...
Genauso ist Set{3,Set{1,2}} nicht typkorrekt.
3.3.8 Mengen- und listenwertige Navigation
Navigation entlang einer Kette von Assoziationen findet in der OCL besondere Aufmerksamkeit, da so die Zustände ganzer Gruppen von Objekten beschrieben werden können, auch wenn der explizit angegebene Kontext nur aus einem Objekt besteht.
Der Ausschnitt des Auktionssystems in Abbildung 3.8 dient als Grundlage die Navigationsmöglichkeiten der OCL/P zu erläutern. Um zu sichern, dass Mitarbeiter der Firma „BAD“ nicht an Auktionen teilnehmen, kann folgende Bedingung gestellt werden:
context Auction a inv:
!("BAD" in a.bidder.company.name)
Dabei kommt entsprechend Abbildung 3.8 eine dreigliedrige Navigationskette zum Einsatz. Während a ein einzelnes Objekt der Sorte Auction darstellt, liefert die Navigation über a.bidder eine Menge von Objekten der Sorte Set<Person>, weil die Assoziation participants in dieser Navigationsrichtung die Kardinalität ⋆ hat. Von der Menge von Personen ausgehend kann mit .company die Menge der diesen Personen zugeordneten Unternehmen beschrieben werden. Das Ergebnis ist weiterhin eine Menge, in der von jeder vorher ermittelten Person das Unternehmen enthalten ist. Der gesamte Navigationsausdruck a.bidder.company.name liefert schließlich eine Menge von Firmennamen, die zur Sorte Set<String> gehören.
Im folgenden Beispiel wird die Assoziation zwischen Personen und Firmen entgegen der angegebenen Navigationsrichtung durchlaufen. In einer Spezifikation ist das ohne weiteres erlaubt, auch wenn die Implementierung es nicht ermöglichen würde:
context Company co inv:
co.name == "BAD" implies co.person.auctions == {}
Eine Navigation entlang einer Assoziation kann auf drei Arten formuliert werden. Ausgehend vom Objekt a der Klasse Auktion wird im Klassendiagramm in Abbildung 3.8 normalerweise mit dem der Ausgangsklasse gegenüberliegenden Rollennamen bidder zu den Personen navigiert. Es ist jedoch auch möglich, den Assoziationsnamen (a.participants) zu verwenden, wenn dieser angegeben ist und zum Beispiel der Rollenname fehlt. Besteht zwischen beiden Klassen nur eine Assoziation und fehlt der Rollenname, so kann auch der gegenüberliegende Klassenname in dekapitalisierter Form verwendet werden: p.message.
Eine Spezifikationssprache wie die OCL wird in verschiedenen Aktivitäten des Softwareentwicklungsprozesses eingesetzt. Insbesondere bei Spezifikation und Entwurf des Systems ist es daher von Interesse, auf gekapselte Attribute einer Klasse zuzugreifen, selbst wenn die Bedingung nicht im Kontext dieser Klasse definiert wurde. Sinnvollerweise werden deshalb die Merkmale protected und private bei der Definition von OCL-Bedingungen ignoriert, so dass auch Attribute und Methoden mit diesen Merkmalen in OCL-Bedingungen verwendet werden können.
Hat eine Assoziation eine andere Kardinalität als 1 oder 0..1, so ist das Navigationsergebnis ausgehend von einem Objekt mengenwertig. Besitzt das Assoziationsende außerdem das Merkmal {ordered}, so ist das Ergebnis eine Liste. Geht die Navigation bereits von einer Menge aus, so wird diese Navigation punktweise angewandt und das Ergebnis wieder zu einer Menge vereinigt. Zum Beispiel kann im Klassendiagramm in Abbildung 3.8 anhand des mengenwertigen Navigationsausdrucks ad.auction.bidder gefordert werden, dass keine Person an mehr als 20 Auktionen beteiligt sein kann:
context AllData ad inv:
forall p in ad.auction.bidder:
p.auctions <= 20
Aus pragmatischen Gründen werden im OCL-Standard [OMG10b] auch keine verschachtelten Mengen bei der Navigation verwendet.14 Bei mengenwertigen Navigationsketten führt das Flachdrücken zwar zu übersichtlicheren und einfacheren Datenstrukturen, hat aber den Nachteil, dass Strukturinformation verloren geht.
Bei einer Navigationskette entlang mehrwertiger Assoziationen wird also nach vorgegebenen Regeln unter Benutzung des Operators flatten flachgedrückt. Diese Regeln werden an folgenden Beispielen erklärt, die in Abhängigkeit des Klassendiagramms in Abbildung 3.8 formuliert sind:
context AllData ad, Person p inv:
let
Company c = p.company; // 1: einfacher Typ
Set<Auction> sa = p.auctions; // 2: mengenwertig
Set<Person> competitors = p.auctions.bidder;
// 3: Kette bleibt mengenwertig
List<Message> lpm = p.message; // 4: wegen Merkmal {ordered}
List<Message> lam = p.auctions.messages; // 5
List<Auction> lma = p.messages.auctions; // 6
in ...
Die Beispiele 1, 2 und 4 zeigen, wie aus einer einelementigen Ursprungsmenge durch eine Navigationskette eine Menge beziehungsweise eine Liste entsteht. Im Beispiel 3 wird eine Kette von zwei jeweils mengenwertigen Navigationen durchgeführt, deren Ergebnis wieder eine Menge ist. Im Beispiel 5 wird ausgehend von der Menge p.auctions von Auktionen eine geordnete Navigation zu den Nachrichten durchgeführt. Das Ergebnis dieser Operation ist eine Liste von Nachrichten, deren Reihenfolge allerdings teilweise unspezifiziert ist. Die Charakterisierung
context Person p inv:
p.auctions.messages == p.auctions.asList.messages;
ist für diese Navigation definierend und zeigt, dass die unspezifizierte Reihenfolge aus der Umwandlung der Menge in eine Liste entsteht. Auch in einer Navigationskette, in der zunächst eine Liste entsteht und dann eine mengenwertige Navigation durchgeführt wird, ist das Ergebnis eine teilweise unterspezifizierte Liste (Beispiel 6).
Der Ausdruck ad.auction.message stellt eigentlich eine Menge von Listen dar, resultiert aber in einer Datenstruktur der Sorte List<Message>. Hier kann zum Beispiel festgestellt werden, wie oft eine Nachricht insgesamt auftritt, nicht jedoch, ob sie in jeder Liste an der ersten Stelle aufgetreten wäre, weil die Information über den Beginn der Einzellisten beim Flachdrücken verloren ging. Um sicherzustellen, dass die Willkommensnachricht bei allen Auktionen gleich versandt wird, lässt sich jedoch statt einer Kette von Navigationen eine Verschachtelung von Quantoren verwenden, in der jede Einzelliste zugreifbar wird:
context AllData ad inv WelcomeMessage1:
forall a in ad.auction:
let List<Message> lmsg = a.message
in
lmsg.isEmpty || lmsg.get(0) == WelcomeMessage
Da verschachtelte Mengen in der OCL zur Verfügung stehen, zeigt nachfolgender Ausdruck, wie die Strukturinformation bei der Navigation erhalten werden kann:
context AllData ad inv:
let Set<List<Message>> slm = {a.message | a in ad.auction}
in
ad.auction.message == slm.flatten
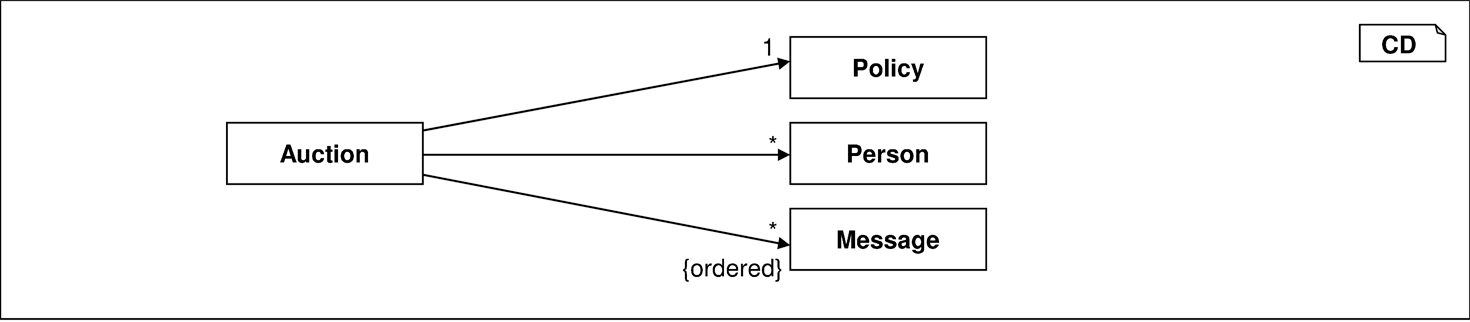
Die Typisierung einer Navigation entlang einer Assoziation kann durch folgende Spezifikation charakterisiert werden, die auf der dargestellten Situation in Abbildung 3.16 basiert. Ausgehend von einem einfachen Objekt hängt das Ergebnis von der Kardinalität der Assoziation ab:
let Auction a = ...;
Policy po = a.policy;
Set<Person> spe = a.person;
List<Message> lm = a.message
in ...
Wird bereits von einer Menge von Objekten ausgegangen, so wird der flatten-Operator genutzt, um die Verschachtelungstiefe beizubehalten. Da die Assoziation zur Policy nicht selbst mengenwertig ist, ist hier der flatten-Operator unnötig. Alle drei nachfolgenden Teilaussagen vergleichen Mengen vom Typ Set<X> mit einem Objekttyp X aus Policy, Person beziehungsweise Message:
let Set<Auction> sa= ...;
in
sa.policy == { a.policy | a in sa } &&
sa.person == { a.person | a in sa }.flatten &&
sa.message == { a.message | a in sa }.flatten
Auch bei bereits tiefer verschachtelten Strukturen wird die Schachtelungstiefe beibehalten. Das heißt insbesondere, dass nicht vollständig flachgedrückt wird. Die nachfolgenden Gleichungen vergleichen Mengen von Mengen Set<Set<X>>:
let Set<Set<Auction>> ssa= ...;
in
ssa.policy == { elem.policy | elem in ssa } &&
ssa.person == { elem.person | elem in ssa } &&
ssa.message == { elem.message | elem in ssa }
Dabei ist der flatten-Operator bereits implizit in den Ausdrücken elem.person und elem.message enthalten beziehungsweise wegen der Kardinalität „1“ in elem.policy nicht notwendig. Nachfolgendes Beispiel mit einer Liste, in der das innere Flattening noch einmal explizit dargestellt wird, zeigt dies:
let List<Set<Auction>> lsa = ...;
List<Set<Person>> lsp = lsa.person
in
lsp == List{ { a.person | a in sa }.flatten | sa in lsa }
Der Unterschied zwischen einer Anwendung des flatten-Operators innen und außen wird erst bei einer Schachtelungstiefe von mindestens drei relevant, wie das Beispiel aus Abbildung 3.17 zeigt.
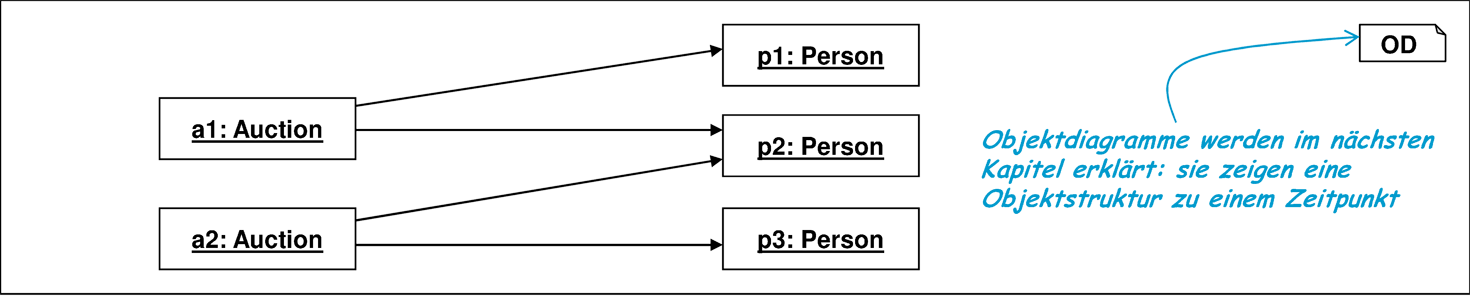
inv:
let Set<Set<Auction>> ssa = { {a1], {a1,a2} };
Set<Set<Person>> ssp1 = ssa.person;
Set<Set<Person>> ssp2 =
{ {a.person | a in sa} | sa in ssa }.flatten
in
ssp1 == { {p1,p2}, {p1,p2,p3} } &&
ssp2 == { {p1,p2}, {p2,p3} }
Dieses Beispiel zeigt auch die teilweise subtilen Probleme, die bei der Spezifikation zu Komplexitäten führen, die ein Modellierer nur in Ausnahmefällen auf sich nehmen sollte. Deshalb wird empfohlen, verschachtelte Container-Strukturen zu vermeiden.
3.3.9 Qualifizierte Assoziation
In Abschnitt 2.3.6 wurden Qualifikatoren eingeführt, um damit den Zugriff auf einzelne Objekte entlang einer mengenwertigen Assoziation zu ermöglichen. Abbildung 3.18 enthält ein Beispiel analog zu Klassendiagramm 3.8 mit Qualifikatoren.
Ausgehend vom AllData-Objekt ad kann durch normale (unqualifizierte) Navigation der Form ad.auction die Menge der Auktionen erreicht werden. Das Ergebnis ist vom Typ Set<Auction>. Die qualifizierte Navigation erlaubt die Benutzung eines zusätzlichen Selektors, um eine bestimmte Auktion zu beschreiben. Wenn acIdent einen Auktionsidentifikator bezeichnet, so wird mit ad.auction[acIdent] die zugehörige Auktion selektiert.15 Dieser Ausdruck evaluiert zu einem Objekt vom Typ Auction. Existiert die Auktion nicht, so hat der Ausdruck den Wert null. Für die weitere Bearbeitung einer qualifizierten Assoziation stehen die Methoden des Typs Map zur Verfügung, mit denen beispielsweise die Menge verwendeter Qualifikatorwerte bestimmt werden kann.
Die nachfolgende Bedingung beschreibt, dass ausgehend vom Singleton ad der Klasse AllData (siehe Bedingung AllDataIsSingleton) jedes Auktionsobjekt unter dem richtigen Auktionsidentifikator angemeldet ist:16
context AllData ad, Auction a inv:
ad.auction[a.auctionIdent] == a;
Das Ergebnis einer qualifizierten Navigation hat einen Elementtyp (hier Auction), weil der Ausgangsausdruck (hier ad) einen Elementtyp hatte und qualifizierte Assoziationen in Navigationsrichtung ausdrücklich mit einer Kardinalität 1 oder 0..1 markiert sind.
Das Merkmal {ordered} beschreibt, dass beide damit markierten Assoziationen ebenfalls als qualifizierte Assoziationen verwendet werden können. Als Qualifikator wird eine ganze Zahl aus dem Intervall 0..message.size-1 verwendet. Das Ergebnis eines qualifizierten Zugriffs hat einen Elementtyp, wie die folgende zu WelcomeMessage1äquivalente Aussage zeigt:
context AllData ad inv WelcomeMessage2:
forall a in ad.auction:
a.message.size > 0 implies a.message[0] == WelcomeMessage
Qualifizierter Zugriff über eine Assoziation ist auch dann möglich, wenn bereits von einem Container ausgegangen wird. In diesem Fall wird die Selektion durch den Qualifikator elementweise vorgenommen. Im folgenden Beispiel wird charakterisiert, wie eine derartige Navigation zu verstehen ist:
inv:
let Set<Auction> sa = ...;
in
sa.message[n] == { a.message[n] | a in sa }
Es gilt für die qualifizierte Navigation ausgehend von Containerstrukturen container:
container.role[qualifier] ==
{ elem.role[qualifier] | elem in container }
3.3.10 Quantoren
Die beiden Quantoren forall und exists erlauben die Beschreibung von Eigenschaften, die für alle beziehungsweise mindestens ein Element aus einer gegebenen Menge gelten müssen.
Allquantor forall
Quantoren können über mehrere Variablen kombiniert werden. Mehrere Allquantoren können zum Beispiel zu einem zusammengefasst werden:17
inv Nachrichten1:
forall a in Auction, p in Person, m in a.message:
p in a.bidder implies m in p.message
Dabei darf in späteren Mengenangaben auf vorher eingeführte Variablen zurückgegriffen werden, denn formal ist obige Invariante Nachrichten1 äquivalent zu:
inv Nachrichten2:
forall a in Auction:
forall p in Person:
forall m in a.message:
p in a.bidder implies m in p.message
Der dritte Quantor dieses Beispiels zeigt auch, dass die Ausgangsmenge, über die quantifiziert wird, nicht nur die Extension einer Klasse, sondern ein beliebiger mengen- oder listenwertiger Ausdruck sein kann.
Der Rumpf einer Quantifizierung ist ein boolescher Ausdruck. Gemäß der gewählten Logik darf die Interpretation dieses Ausdrucks undefinierte Werte liefern, die als false interpretiert werden. Die Bedingung
inv:
forall a in Auction: even(1/0)
ist damit eine syntaktisch korrekte OCL-Formel. Auf den ersten Blick sieht diese Formel unerfüllbar aus, da sie semantisch äquivalent zu
inv:
forall a in Auction: false
ist. Jedoch kann diese Bedingung von Objektstrukturen erfüllt werden, die kein Objekt des Typs Auction enthalten. Ganz allgemein gilt für leere Mengen:
inv:
(forall x in Set{}: false) <=> true
Der Allquantor führt eine oder mehrere neue Variablen ein, deren Werte über eine Menge oder Liste variieren. Er erlaubt so, Aussagen über diese Werte beziehungsweise Objekte zu treffen. Bei komplexeren Ausdrücken sollte einer solchen Variablen auch eine explizite Typisierung hinzugefügt werden, denn der Ausdruck var in klasse ist formal keine Typisierung, obwohl sie nahezu wie eine solche wirkt. Bedingung Nachrichten1 kann also auch formuliert werden als:
inv Nachrichten3:
forall Auction a:
forall p in Person:
forall Message m in a.message:
p in a.bidder implies m in p.message
Im ersten Quantor wurde nur der Typ angegeben, der gleichzeitig als Extension wirkt, im zweiten Quantor wurde auf eine explizite Typisierung verzichtet und im dritten Quantor wurde beides verwendet. Mit dieser Bedingung wird sichtbar, dass der Allquantor eine alternative Schreibweise für die Formulierung des Kontexts einer Bedingung ist. Obige Bedingung Nachrichten3 kann deshalb auch mit Kontext formuliert werden:
context Auction a, Person p inv Nachrichten4:
forall m in a.message:
p in a.bidder implies m in p.message
Hier zeigt sich auch sehr deutlich der Unterschied zwischen einer Kontextdefinition mit context beziehungsweise mit import. Die Bedingung
import Auction a, Person p inv Nachrichten5:
forall m in a.message:
p in a.bidder implies m in p.message
gilt nur für die von außen herangetragenen Objekte a und p, ist also abhängig vom Kontext ihres Einsatzes. Demgegenüber gilt der Rumpf von Nachrichten4 für alle Auktionsobjekte a und für alle Personenobjekte p.
Es ist immer möglich, mit dem Schlüsselwort context eingeführte Kontexte durch Allquantoren auszudrücken. Die Umkehrung für Allquantoren gilt jedoch nicht immer, denn die Grundmenge eines Quantors kann durch einen echten Ausdruck statt nur einer Extension beschrieben werden. Mit folgender Invariante wird die Existenz einer Testauktion gefordert, an der alle Auktionsteilnehmer üben können:
inv Testauktion:
exists m Auction testauction:
testaution.startTime.lessThan(Time.now()) &&
Time.now().lessThan(testauction.closingTime) &&
(forall Person p: !p.auctions.isEmpty
implies p in testauction.bidder)
Dies ist übrigens eine in ihren zeitlichen Implikationen interessante Bedingung, denn die Invarianten-Eigenschaft erfordert, dass jederzeit eine solche Testauktion geöffnet ist. Da Auktionen zu einem festen Zeitpunkt schließen, müssen also regelmäßig neue Testauktionen angelegt werden, um obige Bedingung zu erfüllen.
Existenzquantor exists
Der Existenzquantor ist dual zum Allquantor, in dem Sinne dass er nur von einem Element die Erfüllung einer Eigenschaft fordert. Die Invariante Testauktion hat den Einsatz eines Existenzquantors bereits demonstriert. Auch diese Quantoren können verschachtelt werden. Eine Charakterisierung des Existenzquantors durch den Allquantor kann wie folgt vorgenommen werden:
inv:
(exists var in setExpr: expr) <=>
!(forall var in setExpr: !expr)
Eine Existenzquantifizierung über eine leere Menge hat den erwarteten Effekt:
inv:
(exists x in Set{}: expr) <=> false
Endliche und unendliche Quantoren
Beide Quantoren wurden bisher nur auf endliche Container-Strukturen angewandt. In der Tat ist OCL darauf ausgelegt, mit endlichen Mengen und Listen zu arbeiten. Das hat mehrere Konsequenzen, die bei der Benutzung von Quantoren zu beachten sind. Die Endlichkeit der quantifizierten Menge hat den Vorteil der (zumindest prinzipiellen) Berechenbarkeit, indem die quantifizierte Variable mit allen Werten beziehungsweise Objekten belegt und der Rumpf damit interpretiert wird. Für die quantifizierte Menge ist wesentlich, dass den Klassen, wie zum Beispiel Person, die Extension in Form aller aktuell existierenden Objekte zugeordnet wird, die zwar unbeschränkt aber endlich ist. Würde stattdessen die Menge aller potentiellen Objekte zugeordnet werden, so wäre ein Quantor nicht prüfbar. Als Nebeneffekt wird so auch festgelegt, dass eine quantifizierte Variable weder über den Pseudowert undef für undefinierte Ausdrücke, noch über den Ersatzwert null quantifiziert, sondern nur über tatsächlich existierende Objekte. Es gilt:
inv:
forall A a: a != null
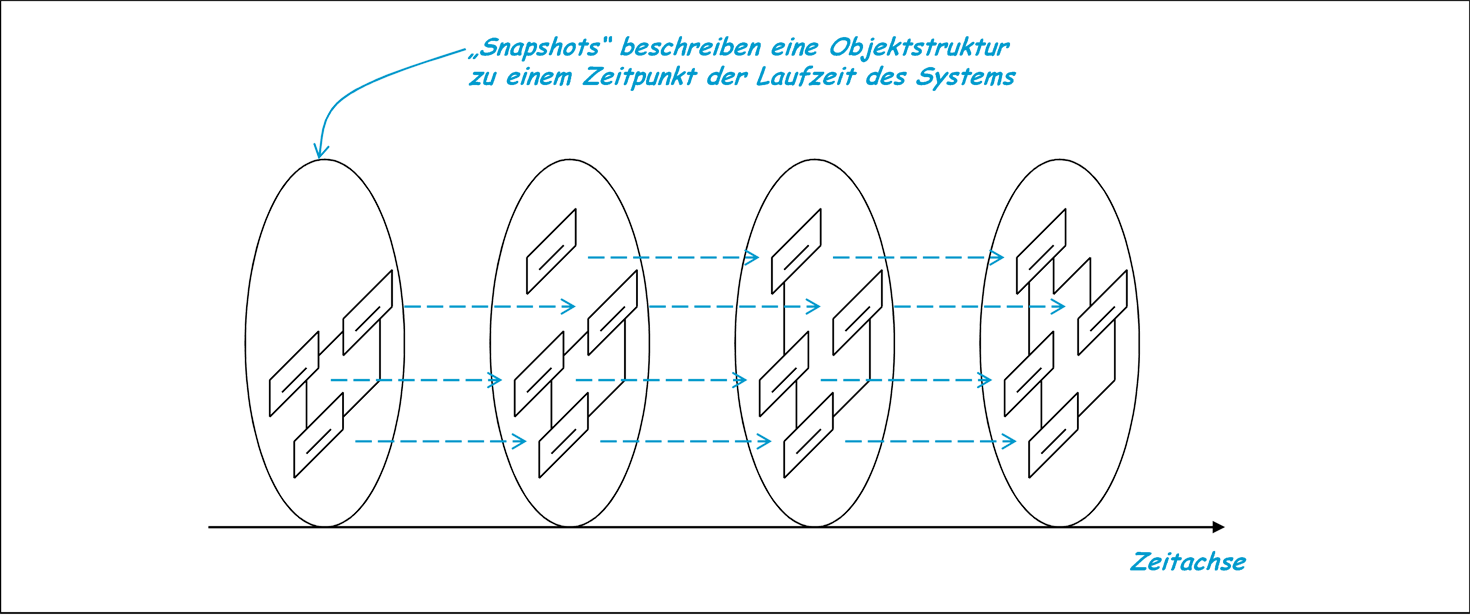
Vom Standpunkt der Logik wird die OCL damit nicht mächtiger als ohne diese endlichen Quantoren. Ein endlicher Allquantor lässt sich im Prinzip auch durch eine Konjunktion ausdrücken. Jedoch gibt es neben den explizit verwendeten Quantoren und der Definition des Kontexts, der ja auch wie ein Allquantor wirkt, einen weiteren, impliziten Allquantor: Eine Invariante gilt für alle auftretenden Objektstrukturen aller Systemläufe gleichermaßen. Abbildung 3.19 illustriert dies. Die Quantifizierung über alle potentiellen Objektstrukturen bleibt implizit. Genau dieser Quantor aber ist unendlich und führt dazu, dass eine Invariante nicht vollständig durch Tests überprüft werden kann, sondern immer wieder neue Systemläufe mit neuen Objektstrukturen auftreten können. Die Korrektheit einer Invariante müsste deshalb über diese Quantifizierung verifiziert werden.
Neben endlichen Mengen von Objekten erlaubt die OCL/P auch die Benutzung von Quantoren über Grunddatentypen. Zum Beispiel ist eine Quantifizierung über den Datentyp int:
inv:
exists int x: x*x > 5
Eine Implementierung, zum Beispiel mit exhaustiver Suche wird normalerweise langsam sein und kann im Falle einer Nichtexistenz eines geeigneten Werts nicht terminieren. Deshalb wird im OCL-Standard [OMG10b] die Quantifizierung über Grunddatentypen und mengenwertige beziehungsweise listenwertige Datentypen abgelehnt. Denn eine Bedingung der Form
inv:
exists int x: x != 5
kann zwei Bedeutungen haben. Ist int die Menge aller zu einem Zeitpunkt in einem System existierenden ganzen Zahlen, so bedeutet obige Bedingung lediglich, dass 5 im System nicht benutzt werden darf. Diese Semantik ist für einen Quantor über ganze Zahlen allerdings sehr unintuitiv und widerspricht der mathematischen Verwendung eines Quantors. In der üblichen mathematischen Interpretation ist stattdessen obige Invariante nicht erfüllbar.
Für Spezifikationszwecke erlaubt die OCL/P die Quantifizierung über unendliche Mengen. Jedoch können diese bei einer Umsetzung in Code oder Tests nicht ohne Umformung übernommen werden. Dasselbe gilt für die Bearbeitung unendlicher Mengen in Mengenkomprehensionen.
inv:
let Set<int> squares =
{ int x | exists y in int: y*y = x && x <= 400 }
in ...
Als Alternative sind endliche Generatoren geeignet, die einen endlichen Ausschnitt bearbeiten:
inv:
let Set<int> squares = { y*y | y in Set{1..20} }
in ...
Besonderer Aufmerksamkeit bedarf auch die Benutzung einer Quantifizierung über Mengen von Objekten. Folgendes Beispiel
inv ListQuantor:
forall List<Person> lp: lp.size != 5
erlaubt mehrere Interpretationen für die Variable lp:
- Alle potentiellen Listen von potentiell existenten Personen-Objekten. Dies ist die mathematische Interpretation, die für Objekte bereits abgelehnt wurde.
- Alle tatsächlich in einem System zu einem Zeitpunkt existierenden Listen. Dies kann wie schon bei der Quantifizierung über Klassen zu Überraschungen führen, wenn das System erweitert wird und an einer neuen Stelle ebenfalls Listen dieser Sorte verwendet werden.
- Alle potentiellen Listen über die tatsächlich zu einem Zeitpunkt existierenden Objekte.
Da in der OCL Container starke Charakteristiken von Grunddatentypen aufweisen (zum Beispiel die Wertorientierung, keine Objektidentität), wird für mengenwertige Quantoren ebenfalls die Interpretation über allen potentiellen Mengen, also Variante 3, verwendet. Damit stellt eine Quantifizierung über Set<Person> eine Kombination der Interpretation eines unendlichen Quantors auf einem Grunddatentyp und einem endlichen Quantor über einen Referenztyp dar. Entsprechend sind Quantoren über Listen unendlich und können daher nur zur Spezifikation eingesetzt werden. Da die Potenzmenge einer endlichen Menge ebenfalls endlich ist, ist die Quantifizierung zum Beispiel über Set<Person> endlich und daher implementierbar. Eine exhaustive Suche ist aber nicht empfehlenswert.
3.3.11 Spezialoperatoren
Der Operator one
Mit den bisher beschriebenen Operationen können viele Bedingungen in bequemer Form formuliert werden. Die OCL/P verzichtet daher auf einen Operator zur Beschreibung der Eindeutigkeit eines mengenwertigen Ausdrucks und zeigt stattdessen, wie sich diese mit den gegebenen Mitteln nachbilden lassen. Folgende Bedingung beschreibt, dass der Login jeder Person eindeutig ist:
context AllData ad inv:
forall String lg in Person.login:
{ Person p | p.login == lg }.size == 1
Operator any
Für die Selektion eines Elements aus einer Container-Struktur gibt es den speziellen Operator any. Dieser Operator ist für Mengen nicht eindeutig festgelegt, wie die folgenden definierenden Gleichungen zeigen:
(any listExpr) == listExpr.get(0);
(any setExpr) == any setExpr.asList;
(any var in collection: expr) == any { var in collection | expr }
Operator iterate
Eine elementweise Bearbeitung von Mengen und Listen lässt sich durch die vorhandenen Komprehensionsformen sehr einfach beschreiben. Eine Verdopplung einer gegebenen Menge von Zahlen m kann zum Beispiel einfach mit {2⋆x | x in m} formuliert werden. Für allgemeinere Fälle bietet OCL den iterate-Operator an, der eine Schleife mit Zustandsspeicher aus der funktionalen wie auch der imperativen Programmierung nachbildet. Der iterate-Operator kann zum Beispiel eingesetzt werden, um die Summe einer Menge von Zahlen zu berechnen:
inv Summe:
let int total =
iterate { elem in Auction;
int acc = 0;
acc = acc + elem.numberOfBids
}
in ...
Die lokal definierte Variable elem iteriert über die gegebene Menge Auction. Die ebenfalls lokal eingeführte Variable acc fungiert als „Zwischenspeicher“ zur Akkumulation des Ergebnisses. Sie wird mit 0 initialisiert. Der Ausdruck acc+elem.numberOfBids wird sukzessive für alle Elemente und dem jeweils aktuellen Zwischenspeicher ausgeführt. Die allgemeine Struktur des iterate-Operators ist charakterisierbar durch:
iterate { elementVar in SetExpr;
Type accumulatorVar = initExpr :
accumulatorVar = expr
}
Das Ergebnis einer Iteration über einer Menge kann uneindeutig sein, da es wie die Konversion zur Liste von der Reihenfolge der Verarbeitung abhängt. Implizit wird bei Mengen wieder eine Umwandlung in eine Liste vorgenommen, weswegen gilt:
inv:
iterate { elementVar in SetExpr;
Type accumulatorVar = initExpr :
accumulatorVar = expr
}
==
iterate { elementVar in SetExpr.asList;
Type accumulatorVar = initExpr :
accumulatorVar = expr
}
Falls die Akkumulation aber kommutativ und assoziativ ist, so ist das Ergebnis ohnehin eindeutig festgelegt. Im Beispiel Summe wurde die Addition verwendet, die diese Eigenschaften erfüllt.
Der iterate-Operator ist ein relativ mächtiger, aber auch implementierungsnaher und wenig intuitiver Operator.18 Es ist zu empfehlen, auf diesen Operator soweit wie möglich zu verzichten.
Operator defined
Der Umgang mit undefinierten Werten führt sowohl in einer Programmier- als auch einer Spezifikationssprache zu zusätzlichem Aufwand und sollte daher weitgehend vermieden werden. An manchen Stellen ist es aber hilfreich oder notwendig, mit undefinierten Werten umzugehen. Dazu wird der spezielle defined-Operator eingeführt, der genau dann true liefert, wenn sein Argument definiert ist. Für undefinierte Argumente evaluiert dieser Operator zu false.
Beispielsweise kann damit die Existenz eines mit einem let-Konstrukt spezifizierten Objekts geprüft werden:
context Auction a inv:
let Message mess = a.person.message[0]
in
defined (mess) implies ...
Der defined-Operator ist in der Lage zu entscheiden, ob ein Ausdruck definiert ist. Aus diesem Grund ist dieser Spezifikationsoperator nicht (vollständig) implementierbar. Jedoch kann aufgrund des in Abschnitt 3.2.2 diskutierten Verfahrens zum Umgang mit undefinierten Werten eine gute Approximation für diesen Operator unter Verwendung des try-catch-Statements aus Java realisiert werden. Damit eignet sich dieser Operator auch als Alternative zum typeif, um zum Beispiel Elemente aus Unterklassen zu erkennen:
context Auction a inv:
let BidMessage bm = (BidMessage)a.person.message[2]
in
defined (bm) implies ...
Die Auswertung der rechten Seite der let-Zuweisung ergibt unter Umständen eine Exception, die in der Variable bm abgelegt wird und eine Repräsentation für einen undefinierten Wert darstellt. Mit defined(bm) entsteht die Möglichkeit auf diesen undefinierten Wert zu reagieren.19
Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012
| << zurück | MBSE Home | weiter >> |