<< zurück

MBSE Home

weiter >>

5.2 Automatentheorie und Interpretation

Die in der UML verwendeten Statecharts sind im Wesentlichen eine um Hierarchie-Konzepte erweiterte Form der endlichen Automaten, bei denen Ausgaben sowohl bei den Zuständen als auch bei den Transitionen möglich sind. Die ausgabebehafteten Moore- beziehungsweise Mealy-Automaten [HU90] werden in diesem Abschnitt in kompakter Form eingeführt und ihre Eigenschaften diskutiert. Die Theorie endlicher Automaten erlaubt diese Diskussion in kondensierter Form, da zum Beispiel das Ein- und das Ausgabealphabet nicht weiter interpretiert werden. Im realen Einsatz werden diese Buchstaben des Alphabets zum Beispiel durch komplexe Methodenaufrufe mit Argumenten und durch in Java-Code formulierte Aktionen ersetzt.

Die nachfolgende kompakte Einführung basiert im Wesentlichen auf [Bra84, HU90, Rum96].

5.2.1 Erkennende und Mealy-Automaten

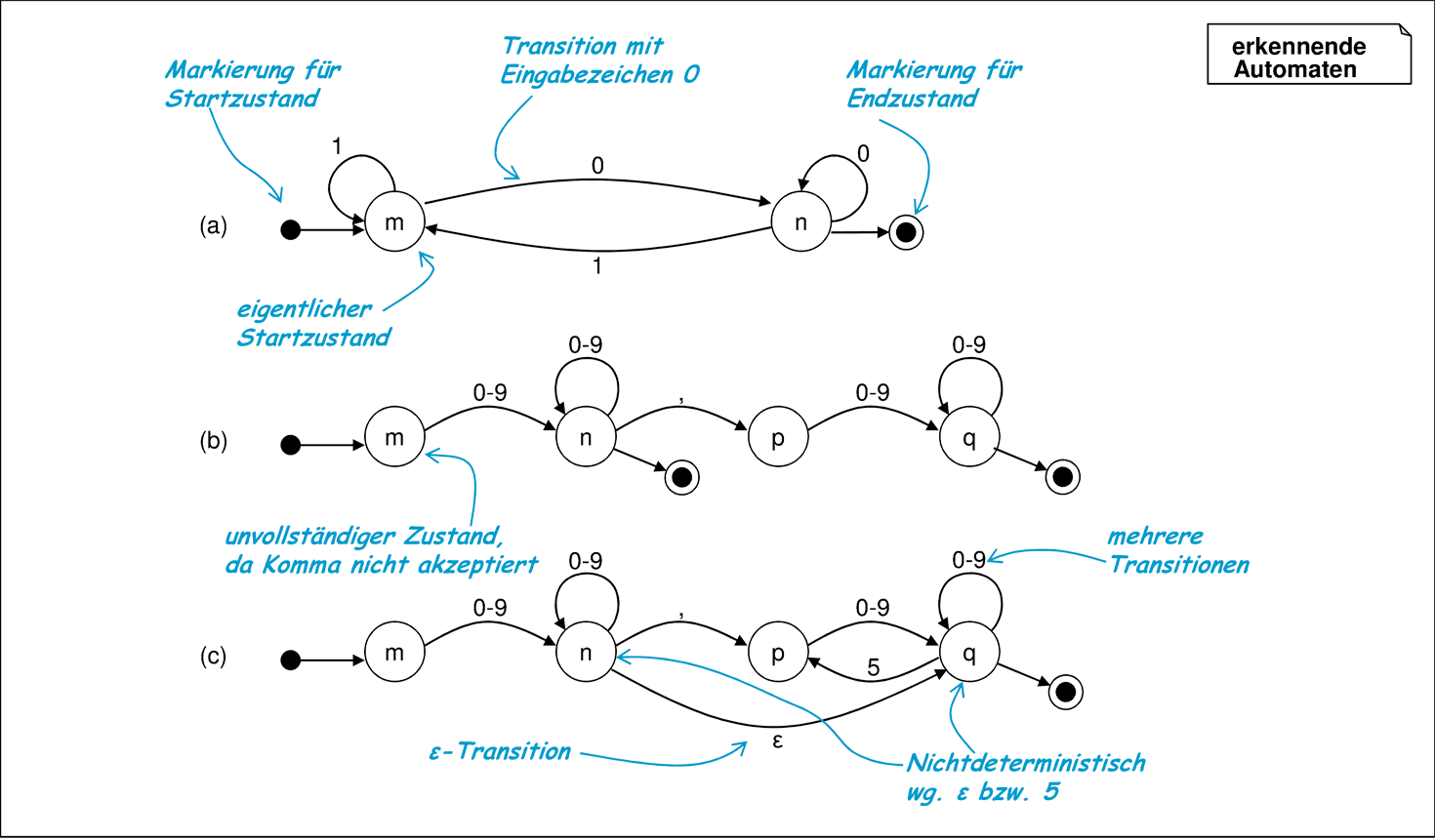
Abbildung 5.2 beinhaltet die Definition von erkennenden Automaten. Eine Transition geht immer von einem Quellzustand zu einem Zielzustand und ist entweder mit einem Eingabezeichen oder mit dem Symbol ε attributiert. Letztere Transitionen heißen spontan, da sie beim Schalten nicht auf ein Eingabezeichen angewiesen sind.

Die Semantik eines erkennenden Automaten besteht aus der Menge aller Wörter des Alphabets E, für die es einen Weg durch den Automaten ausgehend von einem Startzustand in einen Endzustand gibt. Dabei dürfen auch mehrfach Endzustände durchlaufen werden. Abbildung 5.3 beinhaltet drei erkennende Automaten. Der Automat (a) erkennt, ob eine Binärziffernfolge mit einer 0 endet, während die beiden Automaten (b) und (c) Dezimalzahlen mit oder ohne Nachkommaanteil erkennen. Die Semantik eines erkennenden Automaten liegt in der Menge der Wörter, die von einem Anfangszustand in einen Endzustand überführt werden können. Die beiden Automaten (b) und (c) haben daher dieselbe Semantik, auch wenn sie sich in ihren Transitionen unterscheiden. Der Automat (c) beinhaltet außerdem zwei nichtdeterministische Stellen, die zum Beispiel bei der Zeichenfolge 21,0567 mehrere Ablaufmöglichkeiten erlauben.

Wird ein Automat zur Modellierung von objektorientiertem Verhalten verwendet, so spielt die Erkennung von Eingabefolgen eine untergeordnete Rolle. Stattdessen wird die Ausgabe als Reaktion auf das Erkennen eines Eingabeelements und des jeweils angenommenen Zustands als relevant betrachtet. Die Automatenzustände können zum Beispiel auch Zuständen der graphischen Oberfläche entsprechen und für den Nutzer des modellierten Systems so direkt sichtbar sein. Der nachfolgend noch genauer diskutierte Nichtdeterminismus im Automaten spielt deshalb eine wesentlich andere Rolle als bei der Erkennung von Wortmengen.

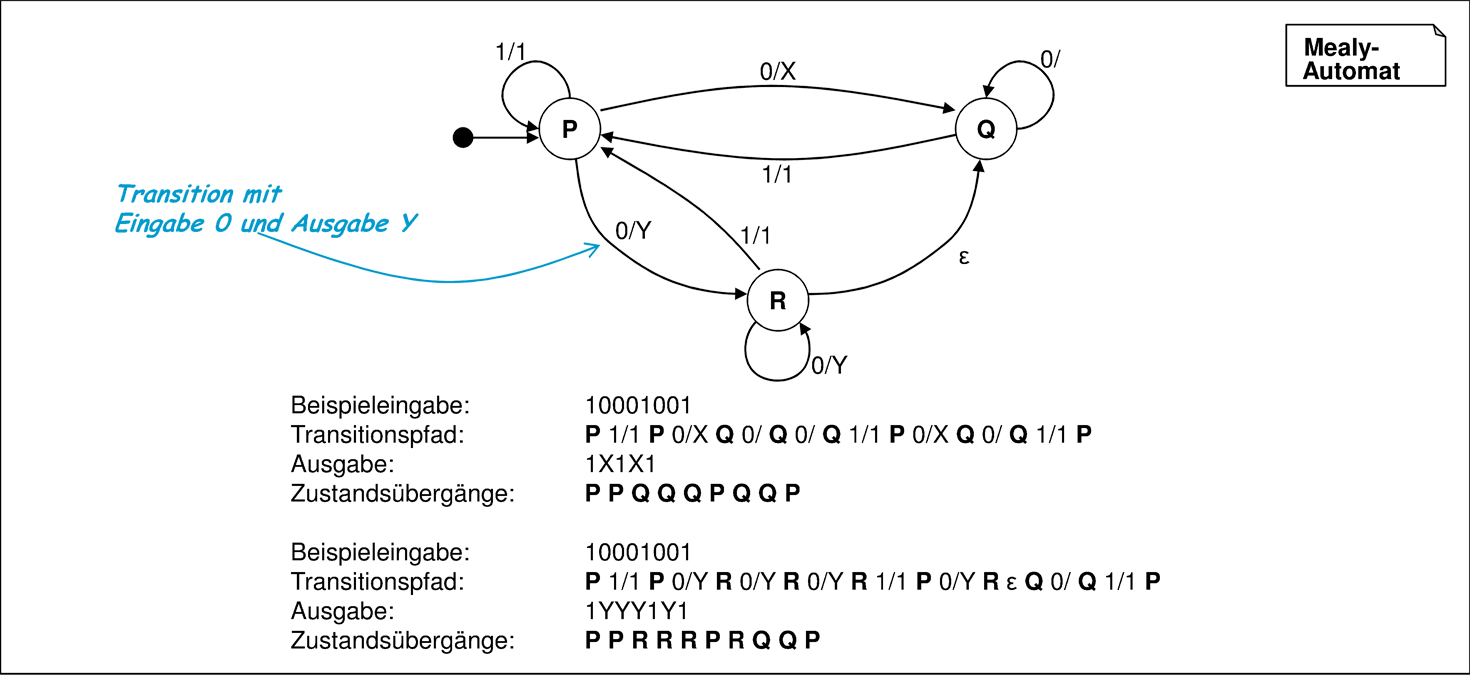
Nach [Bra84] ist ein Mealy-Automat wie der in Abbildung 5.4 eine Erweiterung des erkennenden Automaten, der eine Ausgabe an den Transitionen besitzt. Alternativ wäre es auch möglich gewesen, den erkennenden Automaten um Ausgabe an den Zuständen zu einem Moore-Automaten zu erweitern. Aus der Theorie endlicher Automaten ist bekannt, dass sich beide Erweiterungen nicht prinzipiell in ihrer Beschreibungsmächtigkeit unterscheiden, sondern im Wesentlichen ineinander überführbar sind.

Die Semantik des Mealy-Automaten besteht aus der Relation, die beschreibt, welche Eingabeworte zu welchen Ausgabeworten führen. Ist wie in der objektorientierten Modellierung zusätzlich der Zustandsraum von Interesse, so kann die Bedeutung eines Automaten auf die Menge der möglichen Pfade durch den Automaten erweitert werden. So enthält Abbildung 5.5 einen Mealy-Automaten, der aufeinanderfolgende Sequenzen der Ziffer 0 in der Eingabe durch ein X oder mehrere Y ersetzt. Der im Automat vorhandene Nichtdeterminismus wirkt sich sowohl bei den Zustandsübergängen als auch bei der entstehenden Ausgabe aus. Bei Mealy-Automaten spielen die Endzustände oft keine wesentliche Rolle mehr und werden deshalb häufig nicht angegeben.

5.2.2 Interpretation

Ein Formalismus, wie die Theorie der endlichen Automaten, konzentriert sich auf die Darstellung der für die jeweilige Untersuchung wesentlichen Strukturen. Er ist deshalb geeignet, Fähigkeiten und Begrenzungen von Automatendarstellungen sowie Regeln zur Vereinfachung und sequentiellen oder alternativen Kompositionen zu untersuchen. Ein solcher Formalismus ist ein in sich geschlossenes mathematisches Gebilde, der von der realen Welt abstrahiert und daher auf viele Phänomene der realen Welt angewendet werden kann. In der Modellierung spielt gerade dieser Bezug zur realen Welt eine wichtige Rolle. Um diesen Bezug herzustellen, müssen die einzelnen Konzepte der endlichen Automaten durch Elemente der realen Welt, hier also der objektorientierten Systeme, interpretiert werden. Eine mögliche Interpretation ist etwa die folgende:

• Ein Zustand des Automaten entspricht einem Zustand des Objekts.
• Ein Startzustand ist ein Zustand des Objekts, der unmittelbar nach seiner Erzeugung eintritt.
• Ein Endzustand spielt keine Rolle. Dies reflektiert die in Java vorhandene Garbage Collection, die unerreichbare Objekte in jedem Zustand entfernt.
• Ein Eingabezeichen ist ein Methodenaufruf inklusive der Argumente.
• Ein Ausgabezeichen ist eine Aktion, die im Rumpf einer Methode ausgeführt wird. Sie kann mehrere Methodenaufrufe beinhalten.
• Eine Transition ist die Ausführung eines Methodenrumpfs.

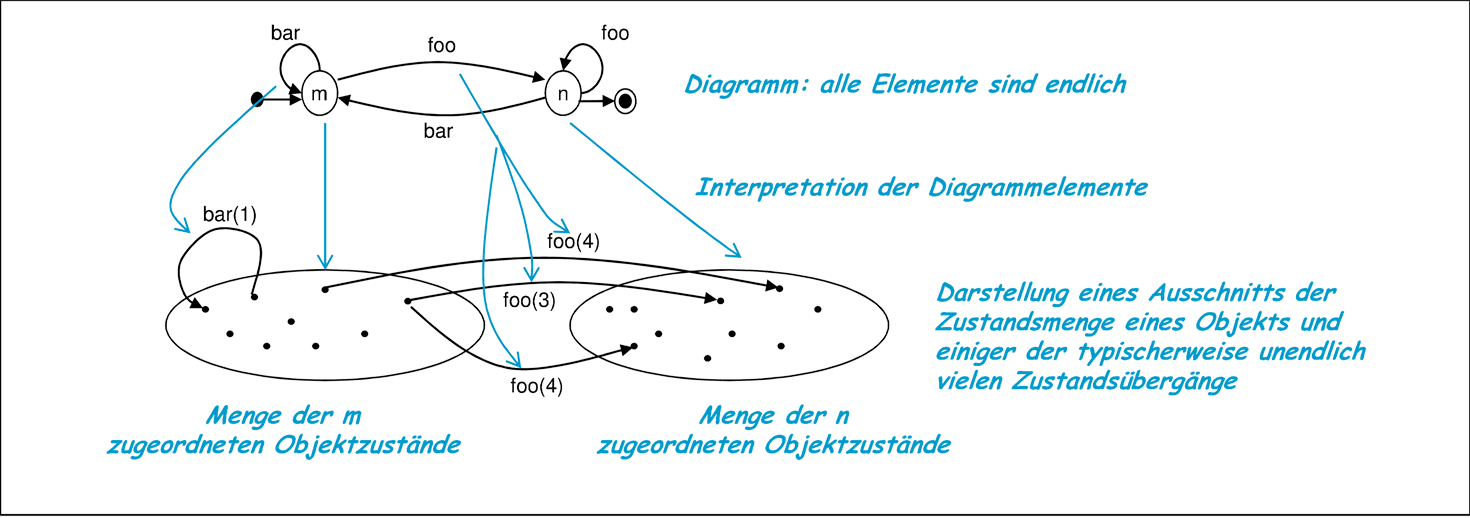
Diese Interpretation erlaubt es, die Erkenntnisse der Automatentheorie auf die zustandsbasierte Modellierung objektorientierter Systeme zu transferieren. Jedoch ist dies bei weitem nicht die einzig mögliche Interpretation. So müssten für praktische Zwecke hier sowohl die Menge der Zustände als auch der Ein- und Ausgabezeichen im Automaten jeweils unendlich sein. Diese unendlichen Mengen sind natürlich nicht geeignet, in einem endlichen und übersichtlichen Diagramm dargestellt zu werden. Die endliche Menge der Diagrammzustände eines Statecharts ist daher anders zu interpretieren.

Wie bereits in [Rum96, Bro97] wird daher eine zweistufige Interpretation eines Statechart-Diagramms vorgenommen. Abbildung 5.6 illustriert, dass die endlich vielen Diagrammzustände und Transitionen eines Statecharts zunächst mit einem unendlichen Mealy-Automaten in Beziehung gesetzt werden. Dieser Mealy-Automat beschreibt das Verhalten eines Objekts.

Die Interpretation eines Diagrammelements durch jeweils eine Menge von Zuständen beziehungsweise Transitionen erzeugt einige Effekte, die bei der Benutzung von Statecharts zur Modellierung zu beachten sind und deshalb nachfolgend diskutiert werden.

5.2.3 Nichtdeterminismus als Unterspezifikation

Wird beispielsweise die Interpretation einer Transition betrachtet, so ist festzustellen, dass auch wenn von einem konkreten Objektzustand mit gegebenen Methodenaufruf ausgegangen wird, eine große Menge von Zielzuständen möglich ist. Eine Transition kann daher hochgradig unterspezifiziert sein. Dies äußert sich dadurch, dass, wie in Abbildung 5.6 illustriert, bei der Interpretation einer Diagrammtransition sehr viele Objektzustandswechsel, die sich jeweils nur in den Zielzuständen unterscheiden, möglich sind. In der Automatentheorie wird diese Form der Unterspezifikation Nichtdeterminismus genannt. Dieser Nichtdeterminismus kann durchaus von methodischem Interesse sein, etwa wenn das Verhalten eines Objekts noch nicht genau festgelegt werden kann oder soll. Ist dieser Nichtdeterminismus jedoch unerwünscht, so kann er zum Beispiel durch zusätzliche OCL-Bedingungen vermieden werden.

Nichtdeterminismus kann jedoch auch bereits im Diagramm selbst auftreten. So können mehrere Diagrammtransitionen von demselben Quellzustand ausgehend dasselbe Eingabezeichen verarbeiten und dabei unterschiedliche Ausgabezeichen produzieren. Diese Form des Nichtdeterminismus kann ebenfalls auf verschiedene Weisen verstanden werden:

1. Die Entwickler haben noch nicht entschieden, welche Transition genau genommen werden soll. Sie werden dazu entweder die Nutzer befragen oder dies der Implementierung überlassen.
2. Der Automat ist eine unvollständige Darstellung des Objektzustands und die Information, die nötig wäre, um genau zu entscheiden, welche Transition zu nehmen ist, wurde im Diagramm abstrahiert.
3. Der Compiler wählt (nach nicht genauer festgelegten Kriterien) eine der Transitionen aus und verwirft alle anderen.
4. Das System ist tatsächlich nichtdeterministisch und darf sich an dieser Stelle abhängig von externen Faktoren oder Zufallsgeneratoren jeweils eine Transition auswählen.

Die Existenz von Nichtdeterminismus bedeutet immer eine Wahlmöglichkeit. Ob diese Wahl vom Entwickler, vom Anwender, vom Compiler oder letztendlich vom System getroffen wird ist dabei nicht festgelegt. Insbesondere bedeutet der Nichtdeterminismus im Automat keineswegs eine notwendigerweise auftretende immer wiederkehrende nichtdeterministische Entscheidung innerhalb des Systems. Ganz im Gegensatz ist in vielen Systemen, insbesondere in Java-Implementierungen, Nichtdeterminismus nur mit zusätzlichem Aufwand zu realisieren. Stattdessen kann dieser Nichtdeterminismus des Automaten im Allgemeinen als Unterspezifikation des Modells verstanden werden.

5.2.4 ε-Transitionen

Eine besondere Form des Nichtdeterminismus bieten die ε-Transitionen. Sie modellieren spontane Übergänge, deren Ursache im Diagramm nicht modelliert ist. Auch dies bietet eine Reihe von Interpretationsmöglichkeiten:

1. Ein Timer ist abgelaufen und führt zu der Transition.
2. Der Automat bietet eine unvollständige Darstellung der Interaktionsmöglichkeiten des Objekts und die Nachricht, die zu dieser Transition führt, wurde nicht modelliert. Allerdings wirkt sich ihr Auftreten auf den sichtbaren Zustand des Objekts aus.
3. Die Transition ist eine logische Konsequenz einer vorhergehenden Transition und wird vom System automatisch ausgeführt. Dadurch lassen sich lange Aktionen in Sequenzen, Verzweigungen und sogar Iteration zerlegen und ε-Transitionen sind als notationeller Komfort interpretierbar.

In nebenläufigen, zeitgesteuerten Systemen ist die Alternative 1 von Interesse, während die Alternative 2 zur Darstellung von Schnittstellenverhalten dient. Die Alternative 3 kann zur Modellierung einzelner komplexer Methoden eingesetzt werden. Diese Statecharts haben weniger den Charakter eines Lebenszyklus darzustellen, sondern wirken als Kontrollflussdiagramm.

Die Zusammenschaltung mehrerer ε-Transitionen zu einer ε-Schleife ist nicht prinzipiell verboten, jedoch auch nicht hilfreich.

5.2.5 Unvollständigkeit

Neben der Möglichkeit, mehrere Transitionen für eine Situation anzugeben, kann auch jegliche Transition fehlen. Der Automat ist dann unvollständig, wie zum Beispiel der in Abbildung 5.3 (b). Im Zustand p ist nicht beschrieben, wie auf das Eingabezeichen „ , “ (Komma) zu reagieren ist. Eine solche Unvollständigkeit kann zum Beispiel auf folgende Weisen interpretiert werden:

1. Das ankommende Zeichen wird ignoriert, indem keine Aktion und keine Zustandsänderung vorgenommen wird.
2. Eine chaotische Reaktion erlaubt einen beliebigen Zustandsübergang und eine beliebige Aktion. Sogar ein „Absturz“ des Objekts beziehungsweise des gesamten Systems ist möglich.
3. Es existiert ein expliziter Fehlerzustand, der eingenommen wird und nur durch eine Rücksetznachricht verlassen wird.
4. Eine explizite Fehlermeldung im Stil des von Smalltalk bekannten „Message not understood“ wird ausgegeben, ohne eine Zustandsänderung vorzunehmen.

Während die Alternativen 1, 3 und 4 typisch für die Behandlung von unvollständigen Automaten bei der automatischen Codegenerierung sind, ist die zweite Alternative aus methodischen Gesichtspunkten von Interesse. Wie in [Rum96] diskutiert, ist der lose Ansatz, der nichts verspricht, was nicht explizit im Diagramm dargestellt ist, besonders geeignet, den Entwickler dazu anzuhalten, robust zu modellieren. Der Modellierer kann sich hier also nicht ausschließlich auf den Codegenerator verlassen. Methodisch ist dieser Ansatz auch deshalb von Interesse, weil das Hinzufügen von Transitionen, um diese Unvollständigkeit zu reduzieren, eine Verfeinerung im Sinne der Präzision des beschriebenen Verhaltens darstellt. Derselbe lose Ansatz wird auch bei Klassendiagrammen verwendet, bei denen der Unvollständigkeits-Indikator „… “ anzeigt, dass weitere im Diagramm nicht genannte Klassen, Methoden oder Attribute existieren können.

Um aber beim Prototyping mit unvollständigen Automaten arbeiten zu können, müssen für Codegeneratoren entsprechende Einstellungsmöglichkeiten existieren, um unvollständige beziehungsweise durch Nichtdeterminismus unterspezifizierte Situationen sinnvoll umzusetzen.

5.2.6 Lebenszyklus

Die in Abschnitt 5.2.5 genannten Möglichkeiten, die Unvollständigkeit eines Automats zu interpretieren, hängen eng damit zusammen, in welcher Form ein Automat als Beschreibung eines Lebenszyklus interpretiert werden kann. Wie in [EE97] diskutiert, gibt es die Möglichkeit, einen Automaten als die Beschreibung der Menge aller möglichen Sequenzen von Methodenaufrufen zu verstehen. Sie beschreibt die externe Sicht eines fiktiven Beobachters, der an einem Objekt feststellt, ob die damit beschriebene Menge von möglichen Aufrufsequenzen eingehalten wurde.

Alternativ dazu gibt es auch die Möglichkeit, einen Automat als die Menge der zugesicherten Sequenzen von Aufrufen zu verstehen. Sie beschreibt die interne Sicht einer Implementierung, die die vom Automat vorgeschriebenen Sequenzen von Methodenaufrufen verarbeiten können muss. Der Implementierer kann im Sinne einer robusten Umsetzung weitaus mehr Aufrufsequenzen zulassen, als dies durch den Automat gefordert ist. Die Sicht der Implementierer und der Beobachter sind kompatibel, da Beobachter als Aufrufer sich bezüglich der modellierten zulässigen Aufrufsequenzen korrekt verhalten und die robuste Implementierung idealerweise nicht benötigen.

Wesentliche Unterschiede in beiden Interpretationen ergeben sich, wenn Transformationen auf Automaten vorgenommen werden, um zum Beispiel das Verhalten zu spezialisieren oder zu ergänzen und zu vererben. Beschreibt ein Automat zugesichertes Verhalten, so dürfen Transformationen, wie die in Abschnitt 5.6.2 beschriebenen Umformungen der Statecharts, nur Verhalten hinzufügen und detaillieren. Dies ist in flexibler Weise nur möglich, wenn der Automat als unterspezifiziert, also mit Interpretation der Chaos-Vervollständigung, verstanden wird. In diesem Sinn ist ein Automat eine Beschreibung einer minimalen Menge von Lebenszyklen des Objekts, der ausgebaut werden kann.

Wird der Automat mit einem Fehlerzustand vervollständigt beziehungsweise nicht akzeptierte Methodenaufrufe ignoriert, so beschreibt der Automat eine maximale Menge von Lebenszyklen. Das heißt, er legt die Menge aller möglichen Aufrufsequenzen fest, die nicht in einen Fehlerzustand beziehungsweise zum Ignorieren eines Methodenaufrufs führen. Die Festlegung der Interpretation von Unvollständigkeit ist also auch eine Festlegung, ob der Automat als minimal zugesicherter oder maximal möglicher Lebenszyklus interpretiert wird.

In beiden Interpretationen aber ist das Verhalten für die durch den Automat beschriebenen Aufrufsequenzen identisch, da es durch eine vorgegebene Transitionsfolge abgearbeitet wird.

In einem nichtdeterministischen Automaten ist es möglich, als Reaktion auf dieselbe Eingabe in unterschiedliche Zielzustände überzugehen. Deshalb kann das nachfolgende Verhalten unterschiedlich sein. Insbesondere gibt es daher Sequenzen von Methodenaufrufen, die bei einem nichtdeterministischen Automaten durch eine Transitionsfolge bearbeitet werden, aber auch in unvollständige Situationen führen können. Um zu verhindern, dass das durch einen Automaten beschriebene Objekt in einem Zustand eine illegale Eingabe erhält, muss die aufrufende Umgebung zum Beispiel durch Nachfrage oder interne Berechnung prüfen, ob ein Aufruf möglich ist.¹

5.2.7 Beschreibungsmächtigkeit

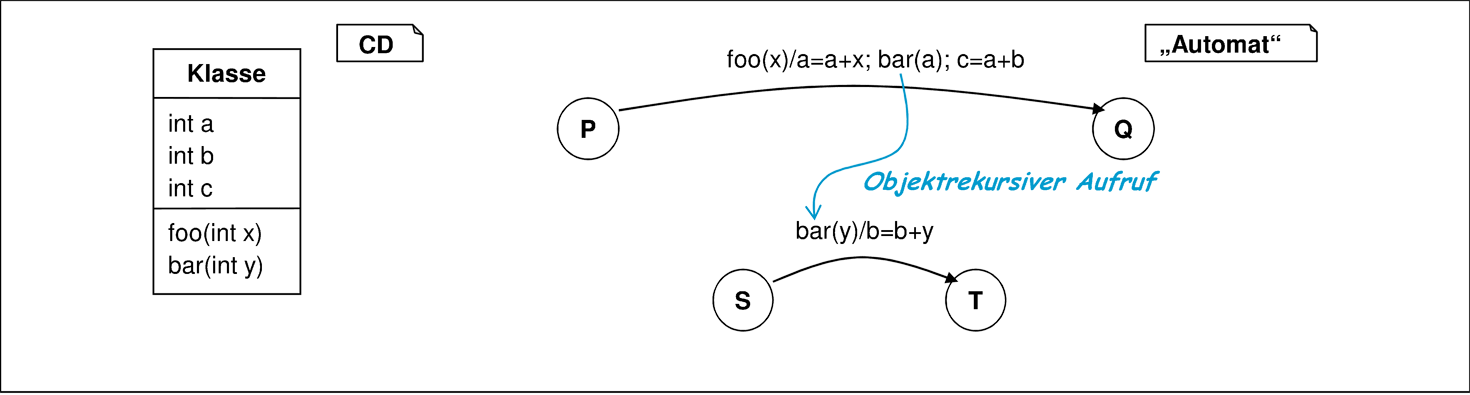
Bekanntermaßen sind endliche Automaten in ihrer Beschreibungsmächtigkeit eingeschränkt. Sie sind geeignet, reguläre Mengen zu beschreiben, aber bereits nicht mehr in der Lage, Klammerstrukturen, wie sie etwa in Java-Ausdrücken vorkommen, vollständig zu erfassen. Das prinzipielle Problem besteht darin, dass ein endlicher Automat nur einen endlichen Zustandsraum besitzt, so dass öffnende Klammern nicht beliebig tief gezählt und damit eindeutig schließenden Klammern zugeordnet werden können. Diese aus der Automatentheorie bekannte Einschränkung manifestiert sich bei der Verwendung von Automaten zur Modellierung objektorientierter Systeme vor allem dann, wenn Methoden eines Objekts weitere Methoden desselben Objekts aufrufen Dabei muss Rekursion nicht notwendigerweise in derselben Methode (Methodenrekursion) stattfinden, sondern es reicht bereits, wenn innerhalb der Methode eines Objekts direkt oder indirekt eine andere Methode desselben Objekts aufgerufen wird. Eine solche Objektrekursion ist in Abbildung 5.7 illustriert, lässt sich aber mit den in Kapitel 6 eingeführten Sequenzdiagrammen wie in Abbildung 6.17 gezeigt noch besser illustrieren.

Die Verschachtelung der Transitionen kann durch den Automat selbst nicht mehr adäquat dargestellt werden. So ist zum Beispiel unklar, ob der durch bar verursachte Zustandsübergang nicht dazu führt, dass der Zielzustand S angenommen wird. Generell ist die Beziehung der Zustände S und T mit dem Zustand Q unklar. Um derartige Problemstellungen zu vermeiden, sind für die Verwendung von Statecharts bei der Modellierung von Objektverhalten im Fall geschachtelter Methodenaufrufe geeignete Einschränkungen zu treffen. So wird zum Beispiel in [HG97] eine Objektrekursion verboten.

Für den Fall, dass die Kommunikation auf asynchronen Nachrichten basiert, reichen jedoch endliche Automaten ohne weiteres aus. In unserem Beispiel 5.7 stellt dann bar(a) nur das Absenden einer Nachricht, nicht jedoch deren Verarbeitung dar. Diese Verarbeitung findet erst nach Ende der aktuellen Transition, also nach Erreichen des Zustands Q statt. Diese Diskussion zeigt, dass der benutzte Kommunikationsmechanismus bei der Zuordnung einer Semantik für Statecharts dann eine Rolle spielt, wenn es Objekten erlaubt ist, sich selbst Nachrichten beziehungsweise Methodenaufrufe in rekursiver Form zu senden.

5.2.8 Transformationen auf Automaten

In der Automatentheorie sind Möglichkeiten zur Transformation, Verfeinerung und Komposition von Automaten detailliert untersucht worden. Diese zunächst zum Zweck der Minimierung oder Entfernung von Nichtdeterminismus und Unvollständigkeit im Automaten eingeführten Transformationen wurden bereits auf verschiedene Varianten zur Modellierung objektorientierter oder eingebetteter Systeme angewandt [Rum96, RK99, KPR97, SPTJ01]. Die im Kontext des Extreme Programming-Ansatzes prominent gewordenen Refactoring-Techniken [Fow99] zeigen, wie hilfreich überschaubare, systematisch ausgeführte Transformationsschritte auf den im Softwareentwicklungsprozess verwendeten Notationen sind. Während sich Refactoring-Techniken auf Java vor allem zur Erhaltung des Verhaltens eignen, können Transformationsschritte auf Automaten auch zur Detaillierung des Verhaltens eingesetzt werden. Einige dieser Transformationsschritte werden in Abschnitt 5.6.2 noch genauer besprochen.

Nachdem in diesem Abschnitt die Grundlagen für Statecharts beleuchtet wurden, werden in den nachfolgenden Abschnitten Statecharts im Detail eingeführt und ihre Interpretation im Kontext der objektorientierten Modellierung diskutiert. Eine kompakte Übersicht der Statechart-Konstrukte ist in den Abbildungen 5.8, 5.9 und 5.10 zusammengefasst.

Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012

<< zurück

MBSE Home

weiter >>