<< zurück

MBSE Home

weiter >>

5.6 Statecharts im Kontext der UML

In den vorhergehenden Abschnitten dieses Kapitels wurde die Statechart-Notation detailliert eingeführt und anhand zahlreicher Beispiele Darstellungsmöglichkeiten demonstriert. Mithilfe mehrerer Stereotypen wurden verschiedene Varianten von Statecharts definiert und ihr jeweiliges Anwendungsgebiet diskutiert. Variationsmöglichkeiten bestehen zum einen in der Semantik der Statechart-Elemente und zum anderen in der Interpretation dieser Elemente im Kontext objektorientierter Modellierung. So wurden zum Beispiel in Abbildung 5.30 mit den Stereotypen ≪prio:inner≫ und ≪prio:outer≫ Möglichkeiten vorgestellt, um die Auswahl sich überlappender Transitionen nach Bedarf festzulegen.

In diesem Abschnitt werden nun einige noch offene grundsätzliche Probleme der Interpretation von Statecharts diskutiert. Dabei werden grundsätzliche Wesenszüge einer Übersetzung in OCL oder in eine Programmiersprache und mögliche Transformationstechniken (Refactoring-Schritte) erläutert.

5.6.1 Vererbung von Statecharts

In UML/P werden die Statecharts grundsätzlich zu Klassen oder Methoden zugeordnet. Zur Darstellung von Statecharts werden OCL-Bedingungen und Java-Codestücke verwendet. Statecharts sind daher immer im Zusammenhang mit anderen Artefakten der Softwareentwicklung zu sehen. In einer Reihe von Publikationen [SHJ⁺94, LW94, LW99, PR94, GKRB96, RK99, KPR97, Rum96, EE97, DL96] werden verschiedene Varianten diskutiert, Statecharts, die einer Klasse zugeordnet wurden, zu spezialisieren und damit einer Detaillierung des Verhaltens zugänglich zu machen. Dazu gehört zum Beispiel die Behavioral Conformity aus [HG97]. Die bei der Vererbung vorgeschlagenen verwendeten Strategien unterscheiden sich teilweise erheblich. Ist zum Beispiel ein Statechart als Schnittstellenbeschreibung einer Klasse gedacht, die vor allem die Aufrufreihenfolge der Methoden beschreibt, so dürfen Transitionen entfernt werden, da dies einer Spezialisierung des Objekts in der Unterklasse entspricht. Ist demgegenüber ein Statechart zur Beschreibung der Implementierung gedacht, so dürfen bei der Vererbung Transitionen hinzugenommen werden, um das Verhalten der Unterklasse robuster gegenüber Fehlern zu machen.

Auch in UML/P haben Statecharts verschiedene Einsatzgebiete. Ein Statechart, das für Testzwecke definiert wurde, kann normalerweise nicht auf Objekte der Unterklasse angewandt werden, da diese ein erweitertes Zustandskonzept und zusätzliche Methoden besitzt. Für die Verwendung konstruktiver, also zur Implementierung gedachter Statecharts, gibt es in der Literatur wie oben beschrieben unterschiedliche Interpretationen.

In der Praxis wird Vererbung von Statecharts selten und dann sehr informell zur Verfeinerung von Verhalten eingesetzt. Meistens wird Verhalten nur redefiniert. Dies bedeutet, dass in der Praxis das zustandsbasierte Verhalten der Ober- und der Unterklasse, wenn beide durch Statecharts modelliert werden, weitgehend unabhängig voneinander ist. Häufig tritt jedoch der Fall auf, dass nur die Oberklasse mit einem Statechart modelliert wird, während die Unterklasse nur die Hilfsfunktionen redefiniert, die keinen Einfluss auf das Zustandskonzept des Statecharts haben. Dadurch wird das Statechart der Oberklasse unverändert übernommen.

Eine weitere Beobachtung zeigt, dass die Klassen, die mit einem Statechart beschrieben werden, häufig keine Unterklassen besitzen, weil sie als komplexe Steuerklassen konzipiert sind und die Variabilität ihres Verhaltens durch Delegation erreichen.

5.6.2 Transformation von Statecharts

Mit dem Erscheinen von [Fow99], das Transformationstechniken für Java-Code enthält, ist deutlich geworden, dass Transformationen auf Modellierungs- und Programmierartefakten eine Verbesserung der Systematik in der Softwareentwicklung erlauben. Die systematische Transformation in kleinen, zusammenfassbaren Schritten ist wesentlich überschaubarer und daher besser planbar als „Big Bang“-Entwicklungen und -Änderungen. Eine Veränderung an durch Klassendiagramme modellierten architekturellen Aspekten des Systems hat meist Auswirkungen an vielen Stellen. Deshalb sind hier kleine, systematische und idealerweise durch Werkzeuge unterstütze Modifikationsschritte ideal. Diese Schritte werden jeweils einzeln durchgeführt und dann sofort auf ihre Wirkung geprüft. Refactoring für Klassendiagramme ist daher wie in [Fow99] beschrieben ein wesentliches Hilfsmittel zur inkrementellen Verbesserung des Systems.

Ein Statechart modelliert demgegenüber nur einen kleinen Ausschnitt des Systems. Es konzentriert sich vor allem auf die Modellierung des Verhaltens eines Objekts und gegebenenfalls einer eng begrenzten Umgebung. Veränderungen im Zustandsmodell oder Verhalten einzelner Objekte können durchaus deutliche Auswirkungen im Gesamtverhalten des Systems haben. Dennoch helfen einzelne Modifikationsschritte, wie etwa die in [SPTJ01, RK99, Rum96, Rum97, EHHS00, EH00, Sch98b] vorgestellten, bei Statechart-Entwicklungen in der Praxis nicht in dem Maße, wie das wünschenswert wäre. Die Erfahrung zeigt, dass gerade die Modifikation des Zustandsraums meist so starke Veränderungen eines Statecharts mit sich bringt, dass das Ausgangsstatechart mit dem neuen Statechart nur wenig gemeinsam hat. Aus pragmatischen Gründen ist es daher häufiger sinnvoll, ein Statechart neu zu entwickeln, statt aus dem alten Statechart herzuleiten.

Auch ist die Anzahl der notwendigen Transformationsregeln, um einen für praktische Anwendungen ausreichend vollständigen Transformationskalkül zu entwickeln, relativ groß. Dies liegt an der großen Anzahl von Modellelementen, die bei Statecharts benutzt werden und der daraus resultierenden Anzahl von möglichen Kombinationen. Aufgrund der aus der praktischen Verwendung heraus motivierten und oben diskutierten Beobachtung wird also auf die Definition eines vollständigen Kalküls zur Transformation von Statecharts verzichtet. Stattdessen wird in diesem Abschnitt ein Satz von Regeln eingeführt, der zur zielgerichteten Transformation von Statecharts dient. Diese Regeln basieren teilweise auf den bereits in früheren Abschnitten in den Abbildungen 5.18, 5.19, 5.22, 5.23, 5.25, 5.26, 5.27, 5.30, 5.37, 5.38, 5.39, 5.40, 5.42 und 5.43 gezeigten Transformationen.

Die Refactoring-Techniken zur Modifikation von Java-Code in [Fow99] dienen ausschließlich zur Erhaltung des extern sichtbaren Verhaltens (siehe [PR01]). Sie fokussieren also auf die Verbesserung von Entwurf und Architektur des Systems, ohne die Funktionalität zu verändern und dienen daher als Grundlage für spätere Erweiterungen der Funktionalität. Der Wunsch zur Transformation eines Statecharts kann jedoch andere Ursachen haben. Da Statecharts primär Verhaltensbeschreibungen sind, ist die Verfeinerung (Detaillierung) des beschriebenen Verhaltens im Statechart gegebenenfalls von gleichem Interesse wie die Erhaltung des Verhaltens. Wie [SPTJ01] zeigt, kann auch die Modifikation des Zustandsraums zum Zweck der Verfeinerung unter der Randbedingung, dass das Verhalten sich nicht verändert, von Interesse sein. Zusätzlich ist zu unterscheiden, ob es sich bei der Modifikation des Statecharts um Anpassungen handelt, die nur das Modell, also die Präsentation betreffen, oder ob diese Anpassungen auch den Zustandsraum und das Verhalten der modellierten Objekte verändern. Diese Unterscheidung ist deshalb wichtig, weil es im Gegensatz zu Klassendiagrammen bei Statecharts sehr viele unterschiedliche Möglichkeiten zur Darstellung desselben Verhaltens gibt.

Nachfolgend werden einige Transformationen für Statecharts vorgestellt, die unter anderem zur Vorbereitung von Codegenerierung dienen, indem sie eine Reduktion der im Statechart verwendeten Konzepte vornehmen.

Vereinfachung von Statecharts

Da Statecharts eine reichhaltige Sammlung von Konzepten zur Verfügung stellen, ist es von Interesse, Transformationsregeln anzugeben, die einzelne Konzepte eines Statecharts eliminieren. Dadurch wird das Statechart weniger reichhaltig in den verwendeten Konzepten und so zum Beispiel für eine Analyse oder Codegenerierung leichter zugänglich. Tatsächlich können die im Folgenden beschriebenen Regeln als erster Schritt in Richtung einer Codegenerierung verstanden werden. Gleichzeitig können diese Regeln auch als definierend für die dadurch bearbeiteten Konzepte verstanden werden. So sind die nachfolgend beschriebenen Eliminationen der Zustandsaktionen und der Zustandshierarchie durch Äquivalenzumformungen beschrieben, die auch in umgekehrter Reihenfolge zur Einführung verwendet werden können.

Die nachfolgend beschriebene Vorgehensweise ist weitgehend automatisierbar. Bei den Schritten 12, 15 und 18 können allerdings Entwurfsentscheidungen getroffen werden oder sind nichtentscheidbare OCL-Bedingungen zu behandeln. Dabei können Optimierungen für eine spätere Codegenerierung vorgenommen werden. Schritte 12 und 15 können aber auch direkt von einem Algorithmus umgesetzt und Schritt 18 ausgelassen werden.

1. Do-Aktivitäten

werden gemäß Abbildung 5.43 eliminiert.

2. Interne Transitionen

werden gemäß Abbildung 5.42 zu echten Transitionen umgeformt. Hat der Zustand mit der internen Transition bereits Subzustände, so werden interne Transitionen lediglich bei den vorhandenen Zuständen als Transitionsschleifen angefügt. Das heißt, Quell- und Zielzustand stimmen jeweils überein, da interne Transitionen keine Zustandsänderung vornehmen.

3. Startzustände innerhalb hierarchischer Zustände

dienen dazu, Transi- tionen, deren Zielzustand der hierarchische Zustand ist, auf einen der Subzustände weiterzuleiten. Gemäß Abbildung 5.25 werden diese Transitionen direkt an Subzustände weitergeleitet, die als Startzustände markiert sind. Die Startzustandsmarkierungen sind dann irrelevant.

4. Endzustände innerhalb hierarchischer Zustände

lassen sich in analoger Form gemäß Abbildung 5.26 entfernen.

5. Zielzustände mit Subzuständen.

Die verbleibenden Transitionen, die noch Zielzustände mit Subzuständen haben, werden auf alle diese Subzustände umgeleitet (und dabei gegebenenfalls vervielfacht). Dabei wird die links angegebene Äquivalenz in Abbildung 5.27 in Kombination mit Abbildung 5.25 genutzt.

6. Quellzustände mit Subzuständen.

In analoger Weise werden die Quellzustände aller Transitionen auf Subzustände umgeleitet und dabei gegebenenfalls vervielfacht. Dabei wird die rechts angegebene Äquivalenz aus Abbildung 5.27 in Kombination mit Abbildung 5.26 angewandt.

7. Wiederholung auf mehreren Hierarchieebenen

kann für die Schritte 3–6 notwendig sein, damit alle Quell- und Zielzustände aller Transitionen einfache Zustände sind (also keine Subzustände mehr besitzen). Start- und Endzustände existieren jetzt nur noch auf oberster Ebene.

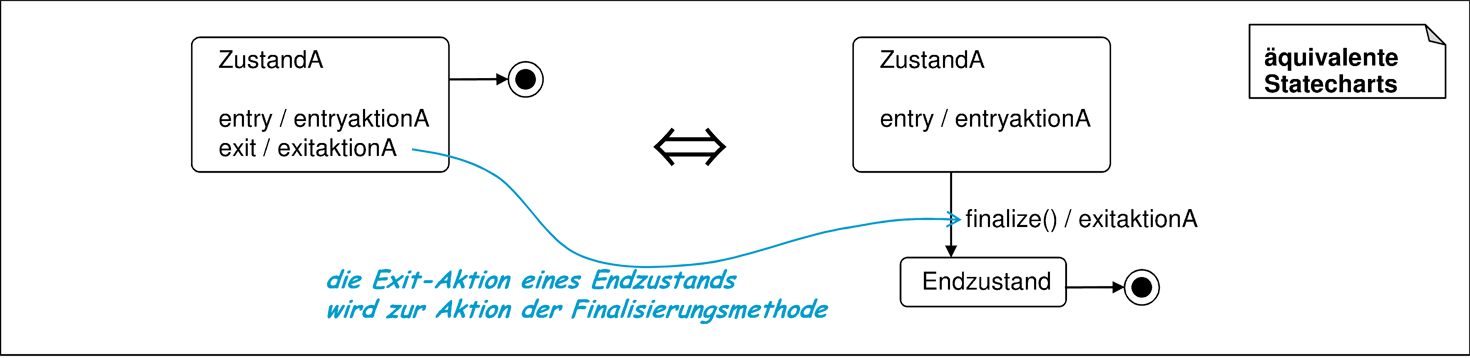
8. Exit-Aktionen

werden gemäß den Abbildungen 5.37 und 5.38 der Aktion der den Zustand verlassenden Transition hinzugefügt. Besitzt ein Endzustand eine exit-Transition, so wird diese gemäß Abbildung 5.44 auch als Aktion des Finalizers aufgefasst.⁶

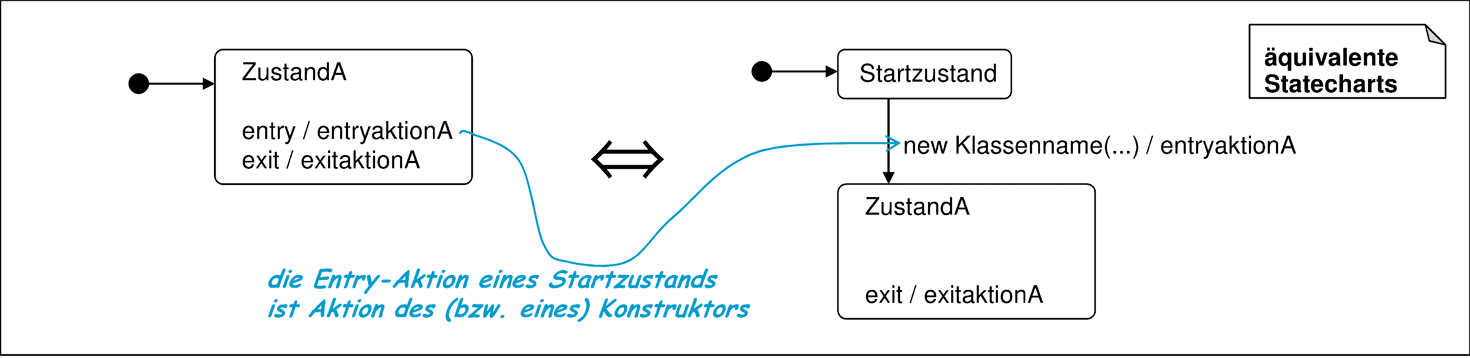
9. Entry-Aktionen

werden in analoger Weise den ankommenden Transitionen hinzugefügt. Entry-Aktionen von Startzuständen werden gemäß Abbildung 5.45 behandelt, indem eine neue Transition davor geschaltet wird, die dem Konstruktor entspricht, der diese entry-Aktion umsetzt. Im Methoden-Statechart wird statt des Konstruktors eine spontane Transition verwendet. Die entry-Aktionen werden dann eliminiert.

10. Zustandsinvarianten von hierarchisch zergliederten Zuständen

wer-
den gemäß Abbildung 5.18 explizit in die Subzustände aufgenommen.

11. Hierarchisch zergliederte Zustände

sind nun irrelevant geworden und werden gemäß Abbildung 5.19 eliminiert. Dabei werden alle Start- und Endzustandsmarkierungen von eliminierten Zuständen auf die Subzustände übertragen.

Im nun erreichten Ergebnis der Transformation sind alle Zustandsaktionen auf Transitionen verschoben worden und alle hierarchisch zerlegten Zustände eliminiert. Die übriggebliebenen atomaren Zustände beinhalten nur noch Zustandsinvarianten.

Behandlung von Zustandsinvarianten

Die Behandlung der Zustandsinvarianten kann nun auf mehrere Arten erfolgen, je nachdem, welche Bedeutung die Zustände besitzen. Deshalb existieren für den folgenden Schritt 12 mehrere Varianten, abhängig davon, mit welchem Ziel das Statechart eingesetzt wird.

Bei der Codegenerierung können Zustandsinvarianten als Zusicherungen für Eigenschaften zu bestimmten Programmpunkten im System eingesetzt werden und daher direkt in den Code übernommen werden. Damit ist die Benutzung der Zustandsinvarianten als Zusicherungen für Tests möglich.

Die Prüfung, ob eine Zustandsinvariante korrekt ist, ist jedoch viel einfacher als die Entwicklung oder Generierung von Code, der sicherstellt, dass die Invariante erfüllt wird. Unter bestimmten, allerdings recht eingeschränkten Umständen, ist es möglich, konstruktiven Code aus einer Invariante zu erstellen. Insbesondere, wenn die Invariante eine Konjunktion von Gleichungen darstellt, die als Zuweisungen interpretiert werden können und in der die auf den linken Seiten stehenden Variablen erst nach ihrer Definition genutzt werden. Eine solche konstruktiv umsetzbare Zustandsinvariante für die Klasse WebBidding (siehe Abbildung 4.32) ist zum Beispiel:

Einerseits kann zwar geprüft werden, ob eine Zustandsinvariante konstruktiv umsetzbar ist. Andererseits ist jedoch im Allgemeinen nicht automatisch erkennbar, ob die Erreichung einer Zustandsinvariante bereits durch die Aktion der eingehenden Transition abgedeckt ist und damit eine Generierung von konstruktivem Code nicht mehr erforderlich ist. Dies kann daher nur der Entwickler selbst entscheiden. Um das Wissen, ob die Zustandsinvarianten eines Statecharts bereits konstruktiv in Aktionen umgesetzt wurden, im Diagramm ablegen zu können, eignet sich ein Stereotyp, der diese Information beinhaltet und der speziell für die Steuerung der Codegenerierung gedacht ist.

In einem einer Klasse zugeordneten Statechart haben Zustandsinvarianten nur zu Beginn und zum Ende einer Methode Relevanz. Sie sind deshalb Teil der Vor- und Nachbedingung einer Methode beziehungsweise der Verarbeitung einer Nachricht. Eine Möglichkeit, diese Zustandsinvarianten in der weiteren Entwicklung zu verwenden, ist daher die Berücksichtigung bei der Definition einer Methode mithilfe eines OCL-Vor-/Nachbedingungspaares.

Bei einem Statechart, das einen Lebenszyklus eines Objekts beschreibt, ist der Objektzustand die einzige Möglichkeit, die Information über den aktuellen Diagrammzustand eines Objekts zu speichern. Deshalb muss aus den Attributen und Links eines Objekts in der Objektstruktur der Diagrammzustand des Objekts berechnet werden können. Dies erfordert in der Implementierung die Verwendung von disjunkten Zustandsinvarianten. Dann ist es möglich, die Zustandsinvariante als Prädikat zu evaluieren und dadurch den Diagrammzustand und die Transition auszuwählen.

Da in der Modellierung mit Statecharts überlappende Zustandsinvarianten erlaubt sind, ist es sinnvoll, diese durch eine geeignete Transformation in disjunkte Invarianten zu überführen. Als nächsten Schritt in der Transformation hin zu einfacheren Statecharts wird deshalb Regel 12 mit den beiden nachfolgenden Varianten vorgeschlagen:

12. Zustandsinvarianten verschärfen,

um sicherzustellen, dass durch Interpretation der Zustandsinvariante der Diagrammzustand, in dem sich ein Objekt befindet, aus dem Objektzustand eindeutig berechnet wird und eine dem Statechart genügende Transition für den ankommenden Stimulus ausgewählt werden kann.

Wenn also ein neuer Stimulus beim Objekt auftritt, kann alleine durch die Zustandsinvariante festgestellt werden, in welchem Diagrammzustand sich ein Objekt befindet und welche Transitionen dadurch schaltbereit sind. In der Praxis gibt es verschiedene Variationen Schritt 12 umzusetzen, von denen zwei vorgestellt werden:

12a. Zustandsinvarianten verschärfen,

indem Aussagen über weitere Komponenten des Objektzustands getroffen werden. Zum Beispiel kann auf die An-/Abwesenheit von Links, die Größe von Containern oder den Inhalt von Attributen Bezug genommen werden.

Die Verschärfung einer Zustandsinvariante mit dem genannten Schritt 12a erfordert jedoch einiges an Wissen des Entwicklers über den Kontext des Statecharts. Bei einer Umsetzung des Statecharts in Code könnten zwar die so entstandenen disjunkten Zustandsinvarianten der Reihe nach evaluiert werden, bis der jeweils aktuelle Objektzustand identifiziert ist, jedoch ist dies im Allgemeinen ineffizient. Ein alternatives Verfahren, das darüber hinaus den Vorteil hat, dass es automatisch durchführbar ist, benutzt ein zusätzliches Attribut zur expliziten Speicherung des jeweils aktuellen Diagrammzustands.

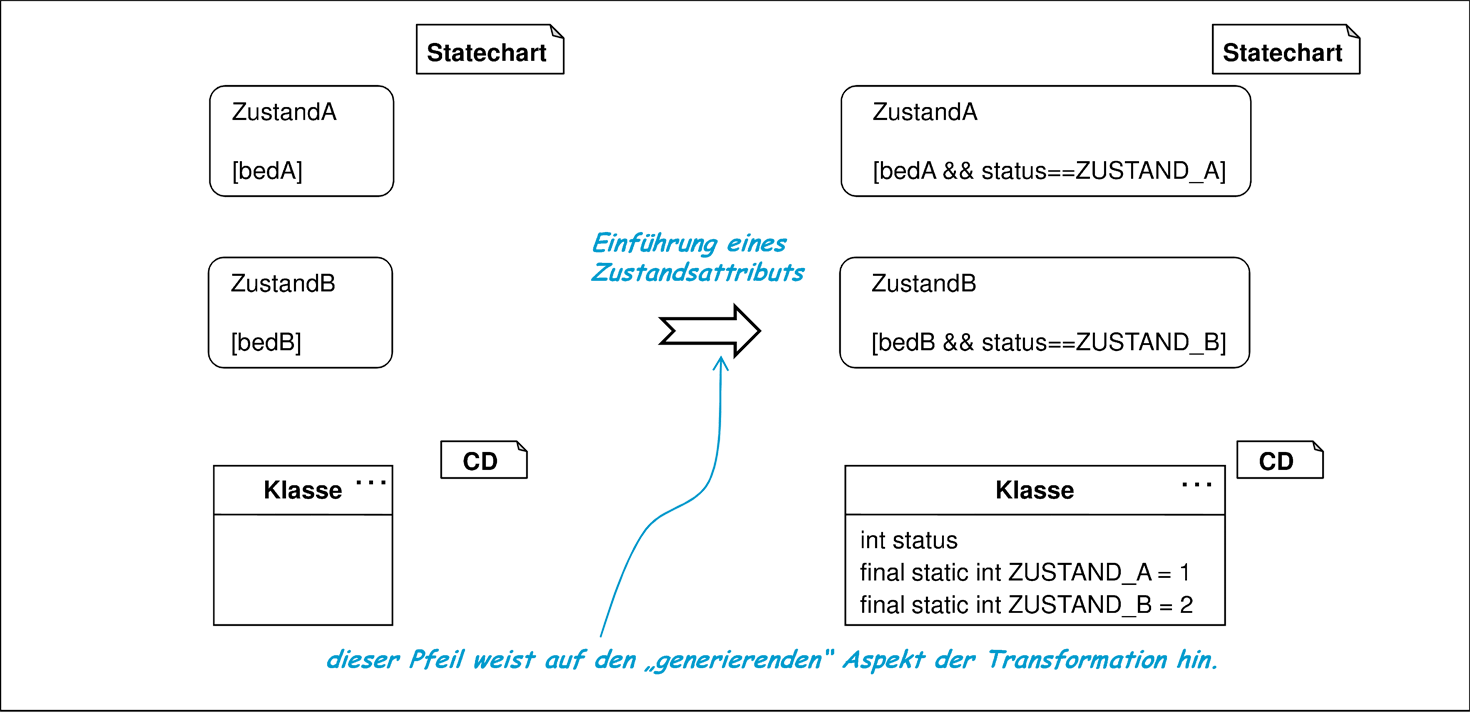
12b. Zustandsinvarianten verschärfen

durch Einführung eines Zustandsattributs gemäß Abbildung 5.46, das den Diagrammzustand eines Objekts explizit speichert.

Die Transformation in Schritt 12b ist eindeutig in Richtung Implementierung gerichtet. Sie ist insbesondere deshalb effizient, weil zur Bestimmung des aktuellen Diagrammzustands nur das Attribut status notwendig ist und eine case-Anweisung zur Diskriminierung verwendet werden kann. Die ursprünglichen Zustandsinvarianten werden dagegen nicht mehr benötigt. Sie können nun in der bereits früher beschriebenen Rolle als Zusicherungen zu Beginn oder nach dem Ende einer dem jeweils aktuellen Stimulus bearbeitenden Methode zu Tests genutzt werden.

Sollten in einem Statechart keine Zustandsinvarianten angegeben sein, so kann dieser Sonderfall überlappender Zustandsinvarianten ebenfalls durch die Einführung eines Zustandsattributs behandelt werden.

Zustandsinvarianten bei Transitionen hinzufügen

Wie bereits bei Abbildung 5.22 diskutiert, wirkt die Zustandsinvariante eines Quellzustands in einer Form, als wäre diese Invariante als Vorbedingung der Transition angegeben. Der folgende Schritt 13 transformiert deshalb die Vorbedingungen aller Transitionen so, dass die Zustandsinvarianten explizit aufgenommen werden:

13. Zustandsinvarianten mit Vorbedingungen konjungieren

gemäß Abbildung 5.22, damit die Vorbedingungen vollständig dargestellt sind.

Durch die explizite Aufnahme der Zustandsinvarianten wird es einfacher, Unvollständigkeiten oder Überlappungen der Schaltbereiche von Transitionen zu erkennen. Die nachfolgenden Schritte können deshalb unter Umständen leichter durchgeführt werden.

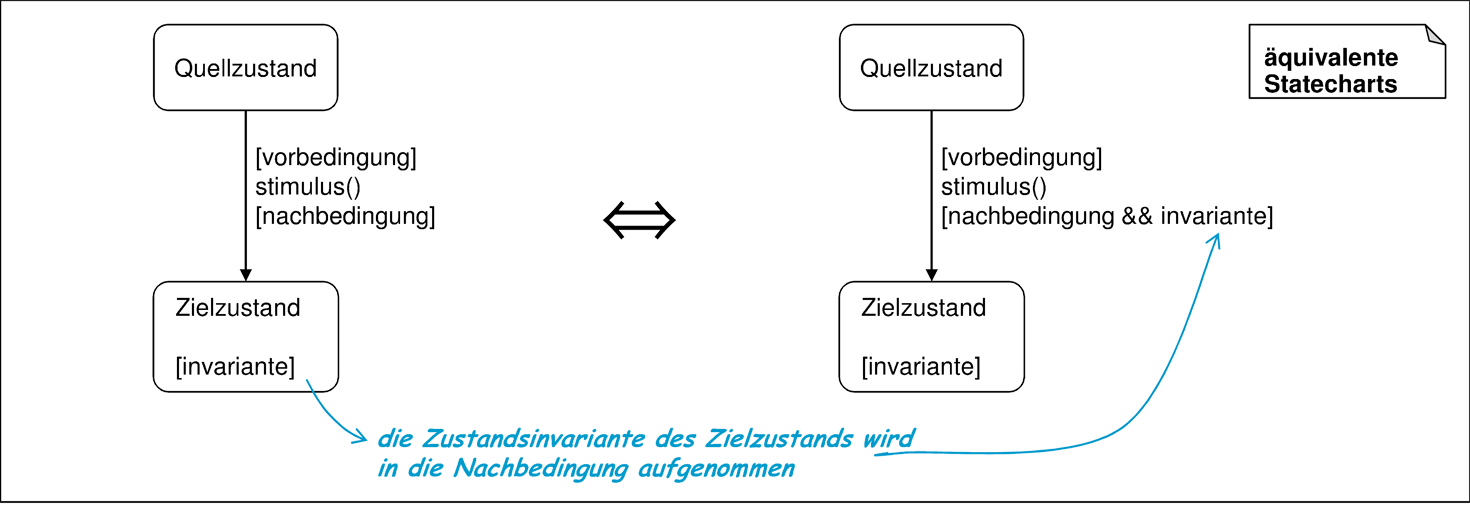
So wie die Zustandsinvariante des Quellzustands einer Transition eine zusätzliche Zusicherung der Transition ist, so ist die Zustandsinvariante des Zielzustands eine zusätzliche Obligation, für deren Erreichung die Transition verantwortlich ist. Diese Obligation läßt sich ebenfalls durch explizite Darstellung in der Aktionsbedingung einer Transition sichtbar machen:

14. Zustandsinvarianten mit Aktionsbedingungen konjungieren

gemäß Abbildung 5.47, damit die Aktionsbedingungen vollständig dargestellt sind.

Unvollständigkeit der Schaltbereiche

Bereits in den Abschnitten 5.2 und 5.4.5 wurden verschiedene Facetten des Nichtdeterminismus und der Unvollständigkeit von Statecharts diskutiert. Dabei wurde auch erörtert, dass die Unvollständigkeit auf verschiedene Arten interpretiert werden kann. Dafür wurden die Stereotypen ≪completion:ignore≫, ≪completion:chaos≫ und ≪error≫ eingeführt. In allen drei Fällen ist es im Prinzip möglich, die Vervollständigung des Statecharts durch Hinzufügen expliziter Transitionen vorzunehmen. Die dabei stattfindende starke Zunahme von Transitionen führt jedoch dazu, dass ein Statechart praktisch nicht mehr lesbar ist. Auch für eine Implementierung ist eine derartige Vervollständigung nicht notwendig, da zum Beispiel bei einer Umsetzung mithilfe einer case-Anweisung eine Unvollständigkeit durch das default-Konstrukt behandelt werden kann. Dies bietet sich für die Stereotypen ≪completion:ignore≫ und ≪error≫ an, denn beide Varianten bieten eine präzise festgelegte definierte Reaktion auf ankommende Stimuli. Für den Stereotyp ≪exception≫ wird zusätzlich ein try-catch-Statement verwendet.

Demgegenüber hat die Chaos-Vervollständigung (Stereotyp ≪completion:chaos≫) das Ziel, Unvollständigkeit als maximal vorhandenen Nichtdeterminismus zu interpretieren. Es ist daher methodisch oft sinnvoll, statt einer Chaos-Vervollständigung eine Vervollständigung durch Auswahl einer sinnvollen Menge von Transitionen vorzunehmen, damit das Statechart auch für die offenen Fälle eine robuste Reaktion zeigt.

Der nachfolgende Schritt 15a beschreibt die Vervollständigung bei einem mit ≪completion:ignore≫ markierten Statechart:

15a. Vervollständigung

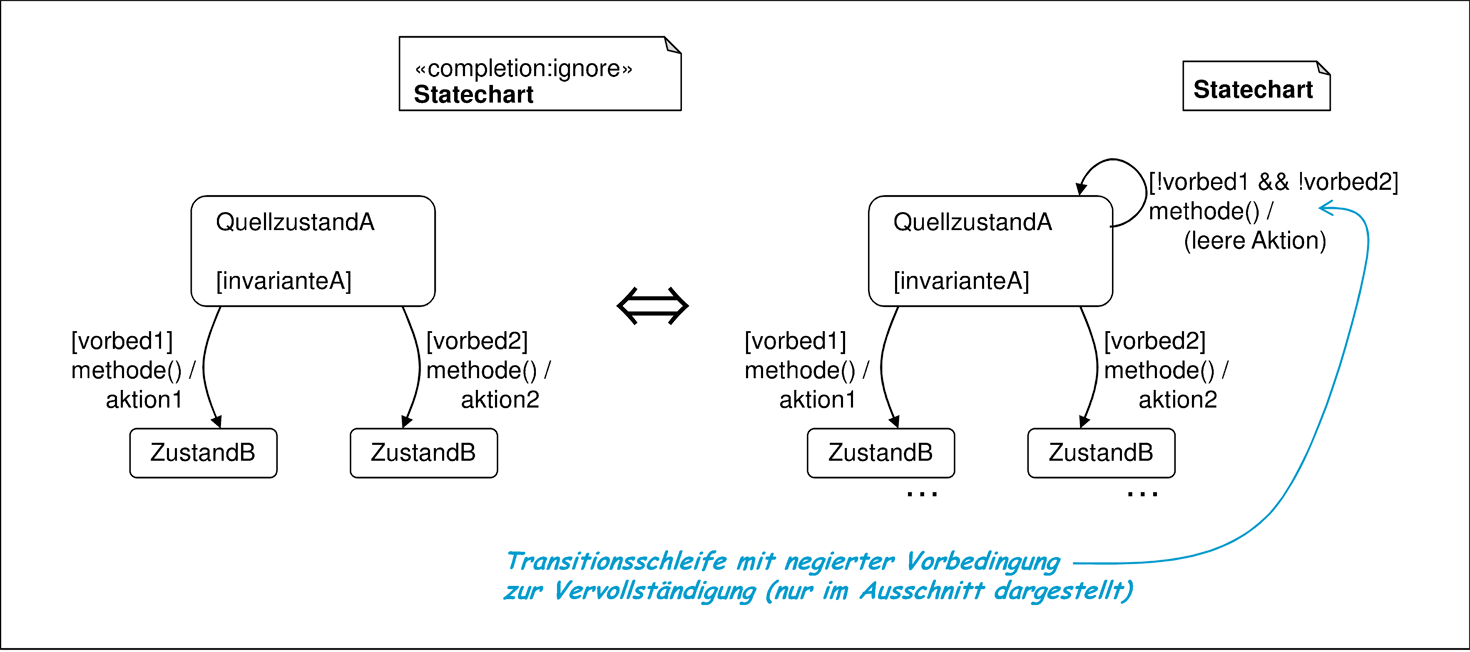
bei mit ≪completion:ignore≫ markierten Statecharts kann durch Einführung expliziter Transitionsschleifen erfolgen, die eine leere Aktion beziehungsweise eine Aktionsbedingung beinhalten, die den Systemzustand unverändert lässt. Dies ist für alle potentiell ankommenden Stimuli und alle Zustände vorzunehmen, für die keine Transition existiert oder die Vorbedingung die Schaltbereitschaft einschränkt.

Wie die Regel zur Durchführung des Schritts 15a zeigt, kann im schlimmsten Fall pro Zustand und pro möglichen Stimulus eine Transitionsschleife notwendig werden. Abbildung 5.48 illustriert anhand eines Beispiels mit zwei Transitionen für denselben Stimulus, wie eine solche Vervollständigung stattfinden kann.

Ob die in Abbildung 5.48 dem Zustand invarianteA hinzugefügte Transition jedoch überhaupt notwendig ist, läßt sich aufgrund der im Allgemeinen nicht automatisiert erkennbaren Erfüllbarkeit von OCL-Bedingungen nur manuell bestimmen. In diesem Fall ist zu entscheiden, ob die Zustandsinvariante invarianteA bereits von den Vorbedingungen der vorhandenen Transitionen vorbed1 || vorbed2überdeckt wird. Nur wenn dies der Fall ist, ist die neu hinzugefügte Transition überflüssig, da sie eine nicht erfüllbare Vorbedingung besitzt. Es ist also zu prüfen, ob:

Wenn dies gilt, kann für die Vorbedingung der neuen Transition gefolgert werden:

Die Vervollständigung bei einem Statechart, bei dem ein Fehlerzustand existiert, erfolgt in analoger Weise:

15b. Vervollständigung

bei Anwesenheit eines mit ≪error≫ markierten Zustands erfolgt analog zu Schritt 15a, indem allerdings alle hinzugefügten Transitionen zum Fehlerzustand führen. Auch der Fehlerzustand wird vervollständigt.

Die folgende Regel für Schritt 15c erlaubt es, wie oben besprochen, statt der vollen Menge von Transitionen, die bei der Chaos-Vervollständigung implizit vorhanden ist, explizit eine geeignete, selbstgewählte Menge von Transitionen hinzuzufügen. Insbesondere besteht dabei völlige Wahlfreiheit bei der Reaktion auf einen ankommenden Stimulus:

15c. Vervollständigung

bei mit ≪completion:chaos≫ markierten Statecharts kann durch Einführung von Transitionen erfolgen, deren Vorbedingungen und Stimuli wie in den alternativen Schritten festgelegt werden. Allerdings besteht die Freiheit, für jede Transition einen eigenen Zielzustand und eine geeignete Aktion auszuwählen. Auch der nichtdeterministische Einbau von Transitionen mit überlappenden Schaltbereichen ist erlaubt (allerdings nur Überlappung zwischen den neuen Transitionen).

Die Vervollständigung in Bezug auf Exceptions kann darauf aufbauend auf dieselbe Weise wie bei Regel 15b erfolgen.

16. Exception-Vervollständigung.

Ist ein mit ≪exception≫ markierter Zustand gegeben, so werden analog zu Schritt 15b mit Exception markierte Transitionen hinzugefügt, die zum Exception-Fehlerzustand führen. Auch der Exception-Fehlerzustand wird vervollständigt.

Nichtdeterminismus reduzieren

Unabhängig davon, ob der Schritt 15 in einer der drei beschriebenen Varianten zur Vervollständigung von Statecharts durchgeführt wurde, kann in dem mittlerweile entstandenen Statechart Nichtdeterminismus in verschiedenen Formen auftreten. Ursachen und Wirkungen vom Nichtdeterminismus in Statecharts wurden bereits in Abschnitt 5.4 detailliert diskutiert. Es gibt zwei wesentliche Gründe, einen im Statechart existierenden Nichtdeterminismus zu behandeln:

1. Ein als Unterspezifikation interpretierter Nichtdeterminismus kann im Verlauf der Softwareentwicklung dazu genutzt werden, zunächst unwichtige Details auf später zu verschieben. Wenn zusätzliche Anforderungen vom Kunden bekannt sind oder wenn weitere Entwurfsentscheidungen getroffen sind, kann durch Reduktion des Nichtdeterminismus das mit dem Statechart modellierte Verhalten verfeinert und detailliert werden.
2. Ist wie in Java die Programmausführung (ohne Threads) deterministisch, so wird bei der Umsetzung eines nichtdeterministischen Statecharts in sequentiell abgearbeiteten Java-Code immer eine Auswahl aus den nichtdeterministischen Alternativen vorzunehmen sein. Eine automatische Auswahl wird oft durch die zufällige Reihenfolge der Bearbeitung der übersetzten Transitionen vorgenommen. Durch explizite Reduktion des Nichtdeterminismus wird jedoch die sonst vom Codegenerator vorgenommene Auswahl durch den Entwickler steuerbar.

Weil die Quellen von Nichtdeterminismus im Statechart vielfältig sind, gibt es eine Reihe von möglichen Modifikationen eines Statecharts, um seinen Nichtdeterminismus zu reduzieren. Ist zum Beispiel das Statechart noch unvollständig und mit ≪completion:chaos≫ markiert, so kann durch einen Wechsel zum Stereotyp ≪completion:ignore≫ oder durch explizite Einführung eines Fehlerzustands mit Stereotyp ≪error≫ der durch die Unvollständigkeit vorhandene implizite Nichtdeterminismus wesentlich reduziert werden.

Ist eine Transitionsaktion unterspezifiziert, so kann durch geeignete Umformung diese Aktion deterministisch gemacht werden.

Eine weitere Quelle von Nichtdeterminismus ist die Überlappung von Schaltbereichen verschiedener Transitionen mit demselben Quellzustand und demselben Stimulus. Ein einfaches Instrumentarium zur Reduktion des hier vorhandenen Nichtdeterminismus ist die in Abschnitt 5.4.4 skizzierte Verwendung von Prioritäten. Es ist jedoch auch möglich, diese Form des Nichtdeterminismus dadurch zu reduzieren, dass die Vorbedingungen dieser überlappenden Transitionen verschärft werden. Die folgende Regel 17 beschreibt die Vorgehensweise:

17. Nichtdeterminismus reduzieren.

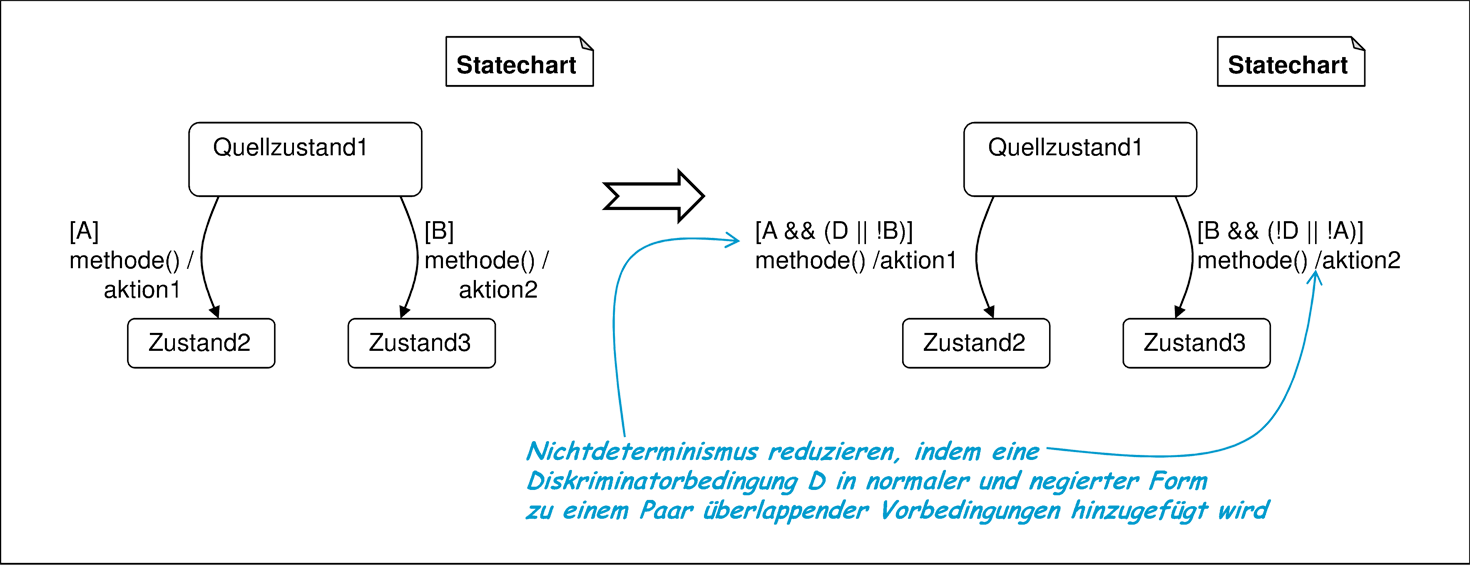
Bei Transitionen mit überlappendem Schaltbereich erfolgt gemäß Abbildung 5.49 durch geeignete Wahl einer Bedingung D, die als Diskriminator zwischen zwei Transitionen wirkt.

Das Verfahren kann paarweise für alle Transitionen mit überlappenden Schaltbereichen angewandt werden.

Die Transformation in Abbildung 5.49 läßt zunächst komplex aussehende Vorbedingungen entstehen, in denen der Diskriminator D den überlappenden Bereich teilt. Der Diskriminator kann im Rahmen syntaktischer Korrektheit frei gewählt werden. Durch geschickte Definition des Diskriminators lassen sich die entstandenen Formeln erheblich vereinfachen. Eine Möglichkeit ist zum Beispiel der Einsatz des Diskriminators true, der die linke Transition unverändert läßt und ihr die Priorität über der nun mit der Vorbedingung B&&!A versehenen rechten Transition gibt.

Transitionen ohne Schaltbereitschaft eliminieren

Durch die zahlreichen bisher durchgeführten Transformationsschritte sind viele neue und veränderte Transitionen entstanden. Insbesondere bei automatisiert durchgeführten Schritten können jedoch Transitionen entstanden sein, die nie schaltbereit sind. Auch durch die Reduktion von Nichtdeterminismus mit der vorher diskutierten Regel 17 kann eine Vorbedingung so eingeschränkt worden sein, dass eine Durchführung der Transition nicht mehr möglich ist. Das gilt zum Beispiel dann, wenn der Schaltbereich einer Transition den einer anderen umfasst. Leider ist die Erkennung von nicht schaltbereiten Transitionen nicht automatisiert durchführbar. Deshalb ist der nachfolgende Schritt ein Optimierungsschritt, der im Allgemeinen vom Entwickler vorgenommen werden muss. Nur in Ausnahmefällen wird das System selbst erkennen, dass eine Transition unnötig geworden ist, weil ihre Vorbedingung äquivalent zu false ist:

18. Transitionen ohne Schaltbereitschaft eliminieren,

da sie keinen Beitrag zum Systemverhalten leisten.

Regel 18 ist besonders interessant in Kombination mit der vorhergehenden Regel 17. Haben zwei Transitionen denselben Schaltbereich, so kann mit Regel 17 zunächst eine Transition auf einen leeren Schaltbereich reduziert werden und dann mit Regel 18 entfernt werden. Im Beispiel in Abbildung 5.49 bedeutet dies, dass A <=> B gelte und dass durch die Wahl des Diskriminators true die Vorbedingung der rechten Transition zu false reduziert wird.

Die Entfernung von Transitionen ist generell dann erlaubt, wenn eine oder mehrere alternative Transitionen existieren, die den Schaltbereich der zu eliminierenden Transition überdecken. Das heißt, dass der Stimulus übereinstimmen muss und dass die Vorbedingung der Transition durch die Vorbedingungen der alternativen Transitionen überdeckt wird, also im Sinne einer Implikation schärfer ist als die Disjunktion der Vorbedingung der Alternativtransitionen. Methodisch ist die Entfernung von unnötigen Transitionen eine Detaillierung des modellierten Verhaltens. Es mag unintuitiv erscheinen, dass durch das Wegnehmen von Transitionen tatsächlich dem Statechart Information hinzugefügt wird. Jedoch ist genau dies der Fall. Nach der Entfernung einer Alternative wird das Verhalten des modellierten Objekts genauer beschrieben. Das Objektverhalten ist damit weniger unterspezifiziert, da es weniger alternative Verhaltensmöglichkeiten besitzt.

Umgekehrt kann auch das Hinzufügen von Transitionen, vor allem beschrieben durch den Schritt 15c, eine Detaillierung des modellierten Systemverhaltens sein. Der wesentliche Unterschied besteht darin, dass das Hinzufügen von Transitionen nur dann erlaubt ist, wenn dafür im ursprünglichen Statechart noch keine Alternative existiert hat, während die Entfernung von Transitionen dann erlaubt ist, wenn mehrere Alternativen existieren.

Nicht erreichbare Zustände eliminieren

Durch Anwendung der Transformationsschritte 17 und 18 können im Diagramm unerreichbare Zustände entstehen. Die Erreichbarkeit eines Zustands ist rekursiv definiert und erfordert die Bestimmung der transitiven Hülle über alle schaltbaren Transitionen ausgehend von der Menge der Startzustände. So können einzelne unerreichbare Zustände leicht dadurch erkannt werden, dass keine Transition dort ankommt. Es kann jedoch auch Regionen von zusammenhängenden Zuständen geben, die sich zwar untereinander erreichen können, jedoch die Region insgesamt unerreichbar ist. Schritt 19 erlaubt diese Diagrammzustände aus dem Diagramm zu entfernen:

19. Nicht erreichbare Diagrammzustände eliminieren,

da sie keinen Bei- trag zum Systemverhalten leisten. Ein Zustand ist erreichbar, wenn er (1) ein Startzustand oder (2) ein Zielzustand einer schaltbaren Transition ist, deren Quellzustand erreichbar ist. Transitionen mit unerreichbaren Quellzuständen werden ebenfalls entfernt.

Ergebnis der Transformation

Nach Durchführung der beschriebenen Vereinfachung des Statecharts entsteht eine flache Struktur, die nur Transitionen enthält, die einen Beitrag zum modellierten Verhalten liefern. Die Zustände beinhalten disjunkte Zustandsinvarianten. Alle Aktionen wurden auf Transitionen verlegt. Die Transitionen sind vollständig in dem Sinne, dass sie die vollständige Vorbedingung und Nachbedingung beinhalten und damit direkt zu einer Umsetzung in Code geeignet sind.

Durch die Entfernung einer Reihe von Statechart-Konzepten ist das Ergebnis leichter einer Analyse oder einer Codegenerierung zugänglich. In den nachfolgenden Betrachtungen wird deshalb von einer vereinfachten Form der Statecharts ausgegangen.

5.6.3 Abbildung in die OCL

Statecharts dienen zur zustandsbasierten Verhaltensbeschreibung von Objekten. Das Verhalten von Objekten wird letztendlich durch die Methoden realisiert, die als Stimuli in den Transitionen verwendet werden. In Abschnitt 3.4.3 wurden OCL-basierte Methodenspezifikationen eingeführt, mit der Methoden ebenfalls spezifiziert werden können. Der dort benutzte Vor-/Nachbedingungsstil zur Spezifikation des Effekts einer Methode entspricht relativ genau der Beschreibung durch eine Transition, wenn zur Modellierung der Reaktion eine OCL-Nachbedingung benutzt wird. Deshalb ist die in Abbildung 5.50 beschriebene Transformation von Transitionen des vereinfachten Statecharts nicht überraschend.

Die in Abbildung 5.50 gezeigte Übersetzung erzeugt pro Transition eine solche Vor-/Nachbedingung. Da in einem Statechart meistens eine ganze Reihe von Transitionen denselben Stimulus enthalten, entstehen so mehrere OCL-Spezifikationen für dieselbe Methode. Die Integration mehrerer solcher Bedingungspaare wurde bereits in Abschnitt 3.4.3 diskutiert. Dabei wurden zwei grundsätzlich unterschiedliche Kombinationsmöglichkeiten erörtert, die auch hier eine wesentliche Rolle spielen.

Wird ein deterministisches Statechart, also ein Statechart, dessen Transitionen keine überlappenden Schaltbereiche besitzen, übersetzt, so entstehen Bedingungspaare, deren Vorbedingungen paarweise disjunkt sind. Die Bedingungspaare können also durch den in Abschnitt 3.4.3 beschriebenen Algorithmus kombiniert werden, indem jeweils die Vorbedingung als Wächter für die Nachbedingung fungiert. Die Disjunktheit der Vorbedingungen stellt sicher, dass maximal eine Nachbedingung zu erfüllen ist und damit keine Inkonsistenzen durch sich widersprechende Nachbedingungen entstehen können.

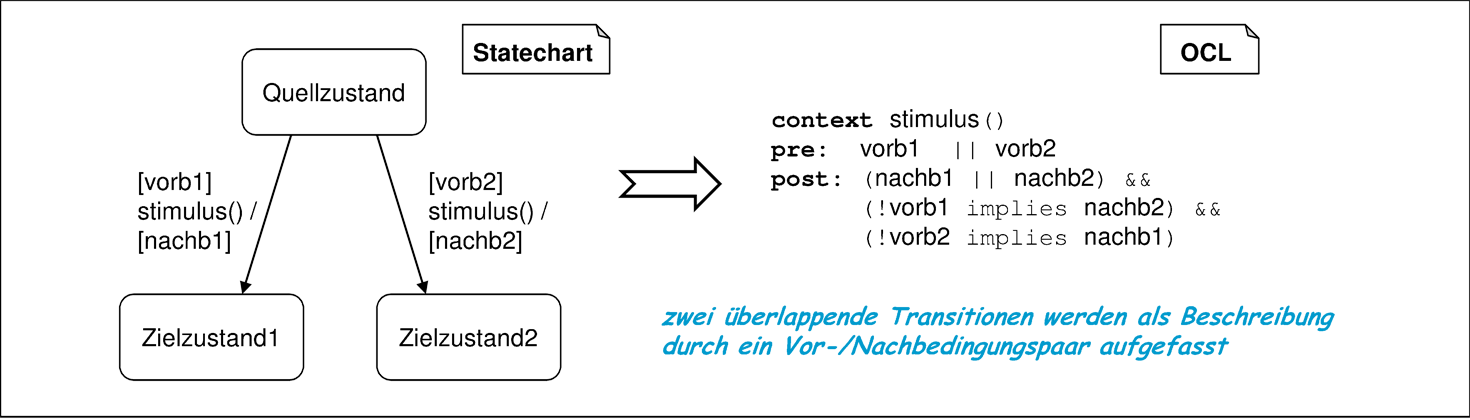
In einem nichtdeterministischen Statechart gibt es jedoch Überlappungen der Schaltbereiche. Transitionen mit überlappenden Schaltbereichen können nicht paarweise in Bedingungen übersetzt werden, denn die Kombination dieser Bedingungspaare würde zu inkonsistenten Nachbedingungen führen. Stattdessen wird eine gemeinsame Übersetzung überlappender Transitionen vorgenommen. Aufgrund der Disjunktheit der Zustandsbedingungen im vereinfachten Statechart können Transitionen mit überlappenden Schaltbereichen nur vom gleichen Quellzustand ausgehen. Die verwendete Übersetzung ist in Abbildung 5.51 anhand von zwei überlappender Transitionen dargestellt. Man beachte, wenn beide Vorbedingungen erfüllt waren, bedeutet die Freiheit der Auswahl von Transitionen, dass danach nur eine der Nachbedingungen erfüllt sein muss, denn es schaltet ja nur eine der Transitionen. Die etwas komplexe Form der Nachbedingung spiegelt dies wider. Eine Anwendung auf mehr als zwei Transitionen ist durch entsprechende Verallgemeinerung oder durch iterierte Anwendung der Regel auf je zwei überlappenden Transitionen möglich.

Die Übersetzung von Transitionsbeschreibungen in OCL-Methodenspezifikationen kann auf zwei Arten eingesetzt werden. Sie kann einerseits als semantische Integration der beiden UML-Teilnotationen, Statecharts und OCL verstanden werden, hat aber andererseits gleichzeitig eine praktische Anwendung. Die semantische Integration in Form dieser Transformation zeigt Beziehungen beider Teilnotationen und führt damit die Semantik von vereinfachten Statecharts auf die OCL zurück. Aufgrund der bereits früher eingeführten Transformation von allgemeinen Statecharts in die vereinfachten Statecharts ist damit eine zusammenhängende Transformationskette der Statecharts in OCL gegeben. Die Bedeutung eines Statecharts kann damit im Sinne einer Semantikdefinition aus der Bedeutung von OCL abgeleitet werden. Eine ähnliche Form der Semantikdefinition für flache Automaten wurde zum Beispiel in [Rum96] mit Zielsprache Focus [BS01] angegeben.

Wird die angegebene Transformation durch ein Werkzeug unterstützt, so können Statecharts im Verlauf des Projekts in OCL übersetzt werden und die dort zur Verfügung stehenden Analyse-, Simulations- und Codegenerierungstechniken auf die so entstandenen OCL-Bedingungen angewandt werden. Insbesondere wird es dadurch möglich, für OCL zur Verfügung stehende Verifikationswerkzeuge auf ein Objektverhalten anzuwenden, das zunächst mit Statecharts beschrieben wurde, und dadurch bestimmte Eigenschaften der modellierten Objekte zu zeigen.

Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012

<< zurück

MBSE Home

weiter >>