<< zurück

MBSE Home

weiter >>

3.4 Statecharts

Statecharts sind eine Weiterentwicklung der Automaten zur Beschreibung von Objektverhalten. Jedes komplexere System besitzt steuernde und kontrollierende Anteile, die mit Statecharts modelliert werden können. Die hier vorgestellte Variante der Statecharts nutzt die OCL als Bedingungssprache und Java-Anweisungen als Aktionen.

3.4.1 Eigenschaften von Statecharts

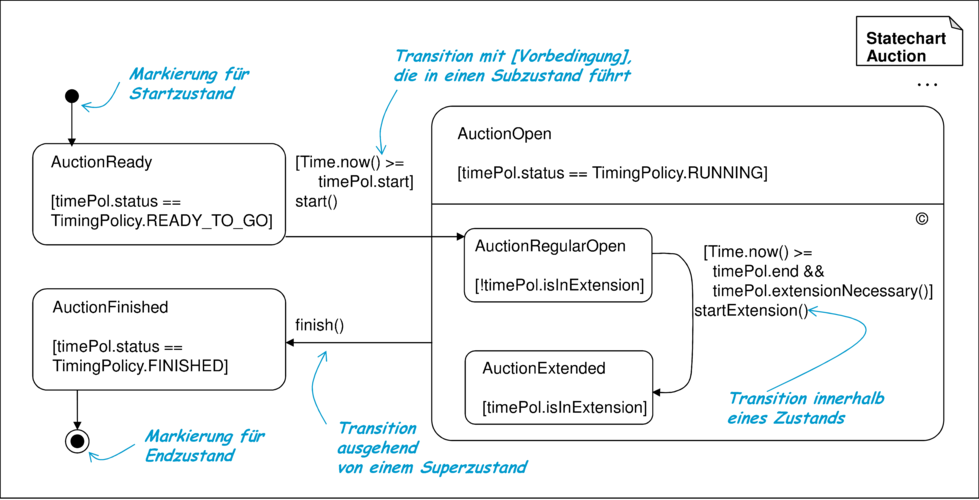
Automaten gibt es in unterschiedlichsten Ausprägungen. So können Automaten ausführbar sein, zur Erkennung von Sequenzen von Buchstaben oder Nachrichten, zur Beschreibung des Zustandsraums eines Objekts oder zur Spezifikation von Antwortverhalten auf einen Stimulus genutzt werden. Der Übersichtsartikel [vdB94] zeigt, dass es für Statecharts eine Reihe syntaktischer Varianten und semantischer Interpretationsmöglichkeiten gibt, die den jeweiligen Anwendungsgebieten angepasst sind. Die Statecharts der UML/P lassen sich durch Steuerung mit geeigneten Stereotypen für die Modellierung, Codegenerierung oder Testfallbeschreibung einsetzen. Abbildung 3.29 zeigt ein Statechart, das eine vereinfachende Abstraktion des Zustandssystems einer Auktion darstellt. Abbildung 3.30 beinhaltet eine überlappende Liste von Aufgaben, die ein Statechart übernehmen kann.

Eine kompakte Übersicht der Statechart-Konstrukte ist in den Abbildungen 3.31, 3.32 und 3.33 zusammengefasst.

Ein Statechart beschreibt das Antwortverhalten eines Objekts, das entsteht, wenn ein Stimulus auf dieses Objekt trifft. Ein Stimulus kann dabei einen Methodenaufruf, eine asynchrone Nachricht oder einen Timeout darstellen. Die Bearbeitung des Stimulus wird atomar durchgeführt. Sie ist also nicht unterbrechbar und nicht parallel zu anderen Transitionen desselben Statecharts.

Während ein Objekt typischerweise einen unendlichen Zustandsraum hat, besteht ein Statechart aus einer endlichen, typischerweise sogar kleinen Menge von Diagrammzuständen. Die Diagrammzustände stellen daher eine Abstraktion des Objektzustandsraums dar. Die Beziehung zwischen Diagramm- und Objektzuständen kann durch Hinzufügen von OCL-Bedingungen präzise definiert werden. Gleiches gilt für die Vorbedingungen und Effekte von Transitionen. Abhängig vom Detaillierungsgrad und der Darstellungsform dieser Bedingungen kann ein Statechart daher als ausführbare Implementierung oder als abstrakte Anforderungsbeschreibung angesehen werden. Statecharts können deshalb von der Anforderungsanalyse bis zur Implementierung eingesetzt werden.

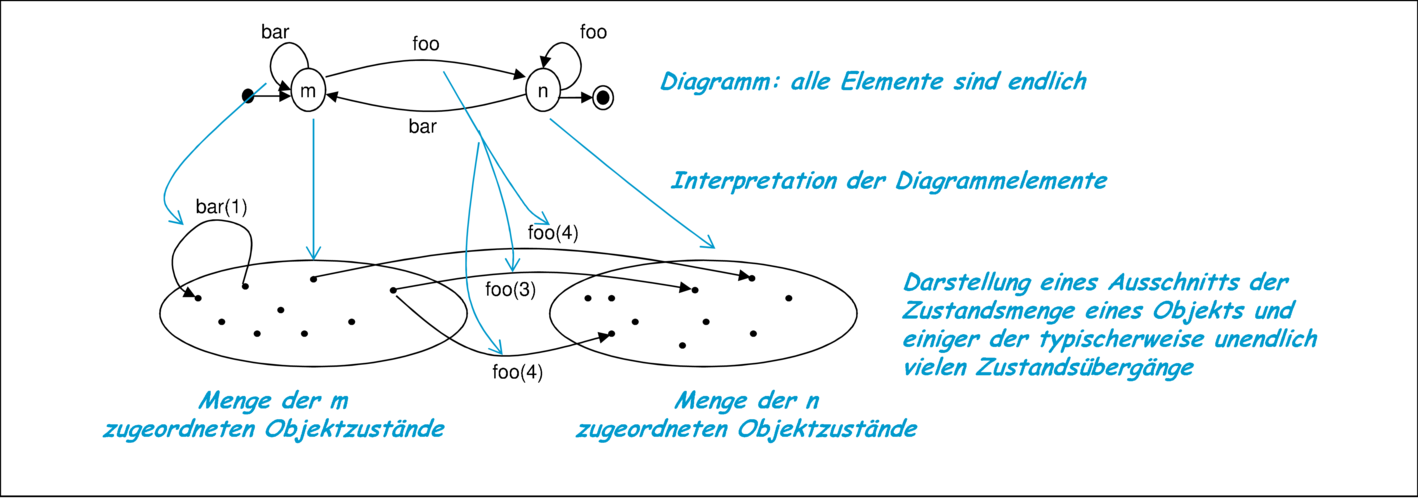
Abbildung 3.34 illustriert, wie die endlich vielen Diagrammzustände und Transitionen eines Statecharts mit einem darunter liegenden unendlichen Transitionssystem in Beziehung gesetzt werden, das das Verhalten des Objekts beschreibt.

Die Interpretation eines Diagrammelements durch jeweils eine Menge von Zuständen beziehungsweise Transitionen hat einige Effekte, auf deren detaillierte Untersuchung in Band 1 hingewiesen wird. Hier seien nur zusammenfassend wesentliche Eigenschaften festgestellt:

• Statecharts basieren auf Mealy-Automaten, die neben der Verarbeitung von Stimuli auch die Ausgabe von Ergebnissen, zum Beispiel in Form von Methodenaufrufen und die Änderung des Objektzustands zulassen.
• Innerhalb des durch das Statechart beschriebenen Objekts existiert keine Parallelität. Die Statcharts der UML/P haben deshalb keine Parallelzustände („And-States“).
• Statecharts erlauben grundsätzlich Nichtdeterminismus. Dieser kann zu echtem Nichtdeterminismus der Implementierung führen, aber auch als Unterspezifikation des Modells interpretiert und durch detailliertere Angaben später behoben werden.
• Spontane (ε-)Transitionen modellieren Beobachtungen, bei der der auslösende Stimulus unsichtbar bleibt (zum Beispiel ein interner Methodenaufruf oder ein Timer). Damit sind spontane Transitionen nur eine besondere Form des Nichtdeterminismus.
• Ein Statechart kann unvollständig sein, indem es für bestimmte Kombinationen aus Zuständen und Stimuli keine Transitionen zur Verfügung stellt. In diesem Fall ist über die Implementierung nichts ausgesagt, also eine robuste Implementierung möglich. Insbesondere wird nicht gefordert, dass die Implementierung den Stimulus ignoriert.
• Mit einem geeigneten Stereotyp lässt sich bei Unvollständigkeit ein spezifisches Verhalten, zum Beispiel durch Transition in einen Fehlerzustand festlegen.

Die beiden primären Aufgaben von Statecharts sind die Darstellung von Lebenszyklen von Objekten und des Verhaltens einzelner Methoden.

3.4.2 Darstellung von Statecharts

Abbildung 3.35 zeigt einen einzelnen Zustand, der von der Klasse Auction eingenommen werden kann und neben dem Namen AuctionOpen eine Zustandsinvariante, je eine entry-Aktion und exit-Aktion sowie eine do-Aktivität beinhaltet.

Da ein Diagrammzustand einer Menge von Objektzuständen entspricht, kann die in OCL beschriebene Zustandsinvariante dazu verwendet werden, diese Beziehung herzustellen. Zustandsinvarianten müssen nicht disjunkt sein. Sind sie disjunkt, so spricht man von Datenzuständen, ansonsten von Kontrollzuständen. Der Datenzustand eines Objekts wird durch die Attribute des eigenen und gegebenenfalls abhängiger Objekte bestimmt. Der Kontrollzustand manifestiert sich im laufenden System zusätzlich durch den Programmzähler und den Aufrufkeller. Eine Zustandsinvariante kann nur über den Datenzustand sprechen.

Hierarchie kann bei Zuständen zur Verhinderung einer Zustandsexplosion eingesetzt werden. Ein hierarchisch unterteilter Zustand hat wie jeder andere Zustand einen Namen und kann eine Zustandsinvariante, eine entry- und exit-Aktion und eine do-Aktivität enthalten. Die flache und hierarchische Darstellung von Zuständen im Statechart sind wie in Abbildung 3.36 illustriert äquivalent, wenn die Zustandsinvarianten entsprechend beachtet werden.

Abbildung 3.29 zeigt die Markierung für Start- und Endzustände auf oberster Ebene. Innerhalb eines hierarchisch zergliederten Zustands können ebenfalls Start- und Endzustände markiert werden. Sie haben dann allerdings eine etwas andere Bedeutung (siehe Band 1).

Wenn das Objekt im Quellzustand einer Transition ist und die Schaltbedingung erfüllt, dann kann die Transition durchgeführt werden. Dabei wird eine Aktion ausgeführt und der Zielzustand der Transition eingenommen.

Stimuli

Für Stimuli, die zur Auslösung einer Transition führen, werden fünf verschiedene Kategorien unterschieden:

• Eine Nachricht wird empfangen,
• ein Methodenaufruf erfolgt,
• das Ergebnis eines Return-Statements wird als Antwort auf einen früher abgeschickten Aufruf zurückgegeben,
• eine Exception wird abgefangen oder
• die Transition tritt spontan auf.

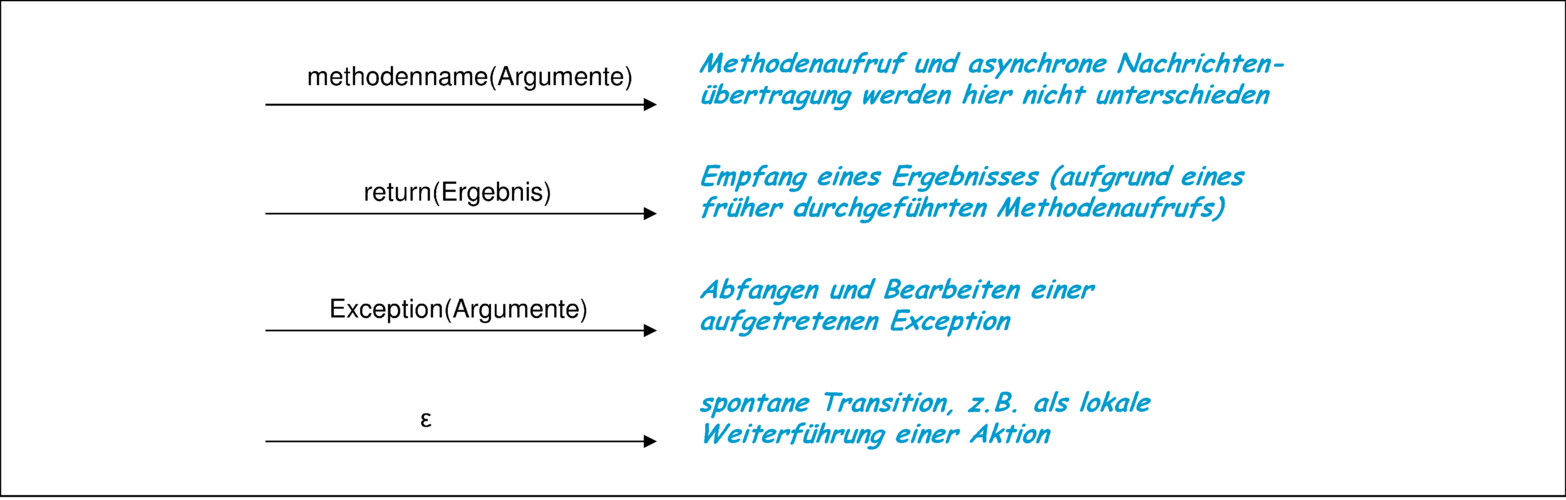
Für das empfangende Objekt macht es keinen Unterschied, ob ein Methodenaufruf asynchron oder als normaler Methodenaufruf übermittelt wird. Im Statechart wird deshalb auch keine Unterscheidung zwischen diesen beiden Arten von Stimuli getroffen. Es ergeben sich deshalb die in Abbildung 3.37 dargestellten Arten von Stimuli für Transitionen.

Schaltregeln

Die Schaltbereitschaft einer Transition lässt sich wie folgt charakterisieren:

1. Das Objekt muss in einem Objektzustand sein, der zum Quellzustand der Transition korrespondiert.
2. Entweder ist die Transition spontan und benötigt daher keinen auftretenden Stimulus oder der für die Transition notwendige Stimulus ist aufgetreten.
3. Die in der Stimulusbeschreibung angegebenen Werte (zum Beispiel Methodenparameter) stimmen mit den tatsächlichen Werten des angekommenen Stimulus überein. Sind in der Stimulusbeschreibung Variablen angegeben, so werden diese mit den tatsächlichen Werten belegt.
4. Die Vorbedingung, die über den Objektzustand und die Parameter des angekommenen Stimulus evaluiert wird, gilt.

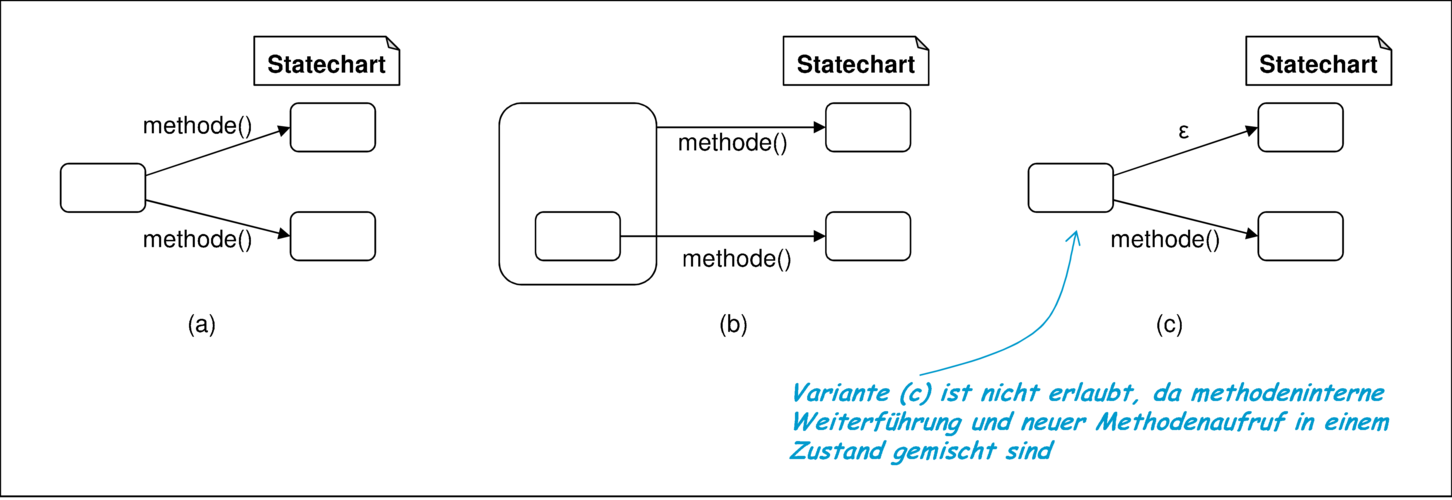
Es kann vorkommen, dass eine Vorbedingung in keiner Situation erfüllt werden kann. In diesem Fall ist die Transition sinnlos, da sie nie durchgeführt wird. Es ist durch Nichtdeterminismus (Unterspezifikation) auch möglich, dass mehrere Transitionen gleichzeitig schaltbereit sind. Deshalb muss eine schaltbereite Transition nicht notwendigerweise auch durchgeführt werden. Nichtdeterminismus im Statechart bedeutet aber nicht notwendigerweise, dass die Implementierung nichtdeterministisch sein muss, denn der Programmierer kann die Unterspezifikation nutzen und selbst die geeignetere Realisierung auswählen. Abbildung 3.38 zeigt zwei erlaubte Situationen überlappender Schaltbereiche.

In beiden Fällen (a) und (b) sind jeweils beide Alternativen möglich. Mit expliziten Prioritäten kann Fall (a) deterministisch aufgelöst werden. Für Nichtdeterminismus auf verschiedenen Hierarchiestufen wird darüber hinaus mit dem Stereotyp ≪prio:inner≫ bzw. ≪prio:outer≫ allgemein festgelegt, ob innere oder äußere Transitionen den Vorzug erhalten.

Im Fall eines unvollständigen Statechart kann ebenfalls durch Einsatz eines Stereotypen das Verhalten präzisiert werden.

1. Mit ≪completion:ignore≫ wird der Stimulus ignoriert.
2. Ein Fehlerzustand wird eingenommen, wenn ein solcher Zustand mit ≪error≫ markiert ist. Für das Bearbeiten von Exceptions kann ein weiterer Zustand mit ≪exception≫ markiert werden.
3. Völlige Unterspezifikation am Statechart wird durch den Stereotyp ≪completion:chaos≫ zugelassen.

Wie in Abschnitt 5.2.6, Band 1 diskutiert, ergeben sich damit Unterschiede in der Interpretation des Lebenszyklus eines Objekts. In den ersten beiden Interpretationen wird der Lebenszyklus als maximal möglich, in der letzten als minimal zugesichert verstanden.

Die Verwendung von ≪completion:chaos≫ ist vor allem in der Spezifikationsphase interessant, wenn durch Verfeinerungen das Verhalten noch detailliert, aber nicht verändert werden soll.

Aktionen

Aktionen beschreiben die Reaktion auf den Empfang eines Stimulus in einem bestimmten Zustand, indem sie dem Zustand als entry- beziehungsweise exit-Aktion oder der Transition als Reaktion hinzugefügt werden. UML/P stellt zwei Arten von Aktionen zur Verfügung. Eine prozedurale Form erlaubt die Nutzung von Zuweisungen und Kontrollstrukturen und eine beschreibende Aktionsform ermöglicht es, den Effekt einer Aktion zu charakterisieren, ohne festzulegen, wie diese Aktion tatsächlich realisiert wird.

Prozedurale Aktionen werden mit Java realisiert, beschreibende Aktionen („Aktionsbedingungen“) mit OCL spezifiziert. Abbildung 3.39 beinhaltet einen Ausschnitt aus einem Statechart für die Klasse Auction, in der eine Transition mit prozeduraler Aktionsbeschreibung und einer Nachbedingung zu sehen ist.

Aktionsbedingungen können einerseits als redundantes Addendum zu Aktionsanweisungen formuliert werden, um damit zum Beispiel bei Tests eingesetzt zu werden, und andererseits können Aktionsbedingungen die Anweisungen ergänzen. So kann ein Teil des Verhaltens bereits prozedural festgelegt und ein anderer Teil noch durch eine OCL-Bedingung beschreibend charakterisiert sein.

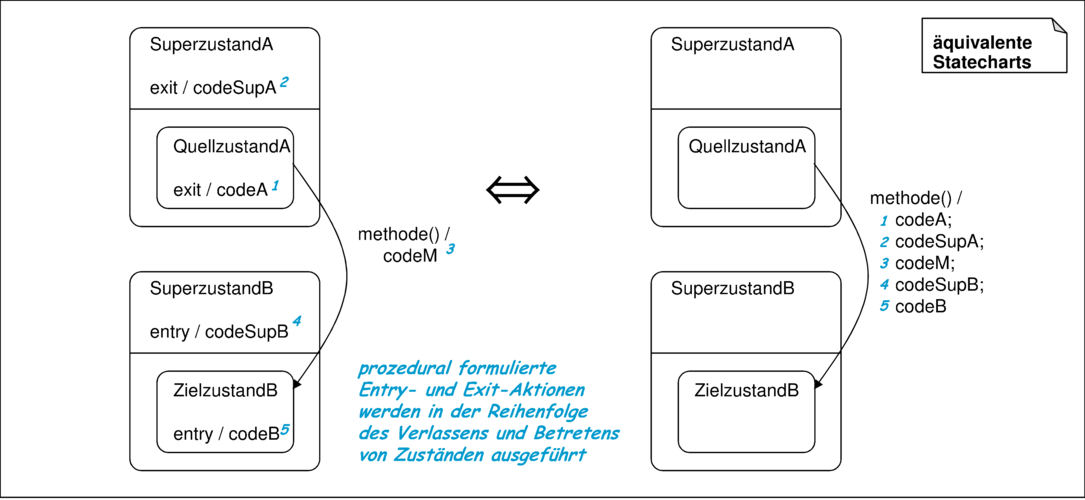
Die Kombination von entry- und exit-Aktionen aus Zuständen und Transitionsaktionen hängt von der Form der vorgegebenen Transition ab. Abbildung 3.40 zeigt den Transfer prozeduraler Aktionen auf die Transitionen und demonstriert, in welcher Reihenfolge entry- beziehungsweise exit-Aktionen in hierarchischen Zuständen ausgeführt werden. Prozedurale Aktionen werden also sequentiell komponiert.

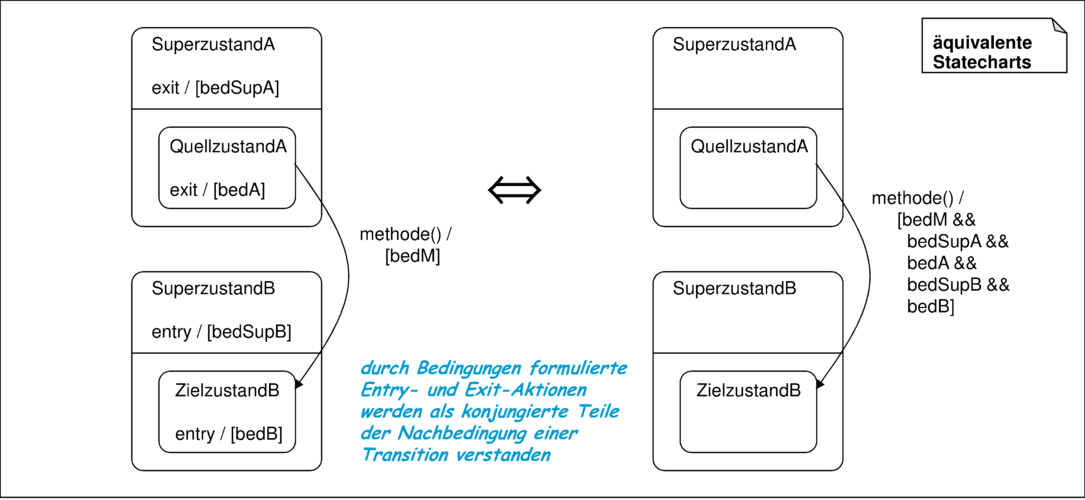
Sind die Aktionen eines Statecharts durch OCL-Aktionsbedingungen spezifiziert, so wird, wie in Abbildung 3.41 gezeigt, statt der sequentiellen Komposition die logische Konjunktion verwendet.

Eine Alternative zur logischen Komposition ist in Band 1 erklärt und charakterisiert eine abschnittsweise Gültigkeit der Bedingungen, die zum Beispiel bei Transitionsschleifen notwendig ist.

Weiterführende Konzepte

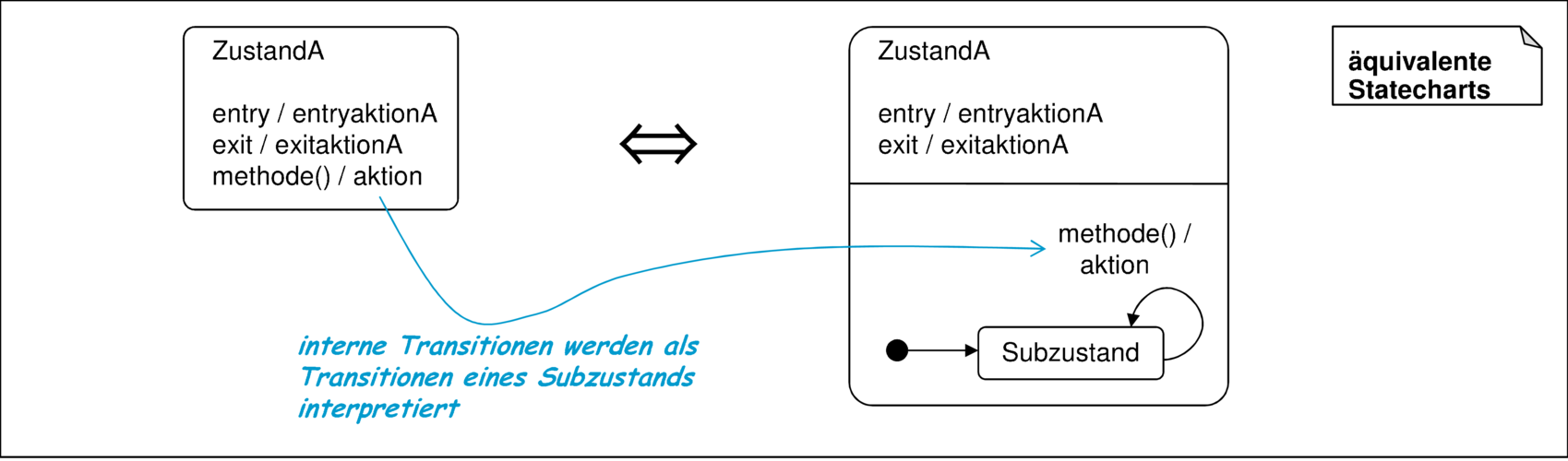
Zustandsinterne Transitionen sind eigenständige Transitionen, bei denen die entry- oder exit-Aktion des Zustands nicht durchgeführt werden. Abbildung 3.42 zeigt, wie eine zustandsinterne Transition verstanden werden kann.

Wenn ein Zustand eine Situation des Objekts repräsentiert, in der eine Aktivität herrscht, zum Beispiel eine Warnmeldung blinkt, kann sie durch eine do-Aktivität beschrieben werden. Abbildung 3.43 charakterisiert deren Interpretation durch einen Timer.

Die in den beiden Abbildungen 3.42 und 3.43 eingeführten Konzepte werden durch Transformation auf bereits vorhandene Konzepte der Statecharts erklärt. In Band 1 ist ein aus 19 Regeln bestehendes Transformationssystem angegeben, das Statecharts vollständig auf flache Mealy-Automaten reduziert und so für eine weitere Bearbeitung einfacher zugänglich macht. Damit besitzen Statecharts einen Transformations-Kalkül, der für die semantikerhaltende Verfeinerung geeignet ist.

Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012

<< zurück

MBSE Home

weiter >>