3.2 Object Constraint Language
Die Object Constraint Language (OCL) ist eine eigenschaftsorientierte Modellierungssprache, die eingesetzt wird, um Invarianten sowie Vor- und Nachbedingungen von Methoden zu modellieren. Die in
der UML/P enthaltene OCL/P ist eine syntaktisch an Java angepasste und erweiterte Variante des OCL-Standards.
3.2.1 Übersicht über OCL/P
Abbildung 3.10 erläutert die wichtigsten Begriffe der OCL.
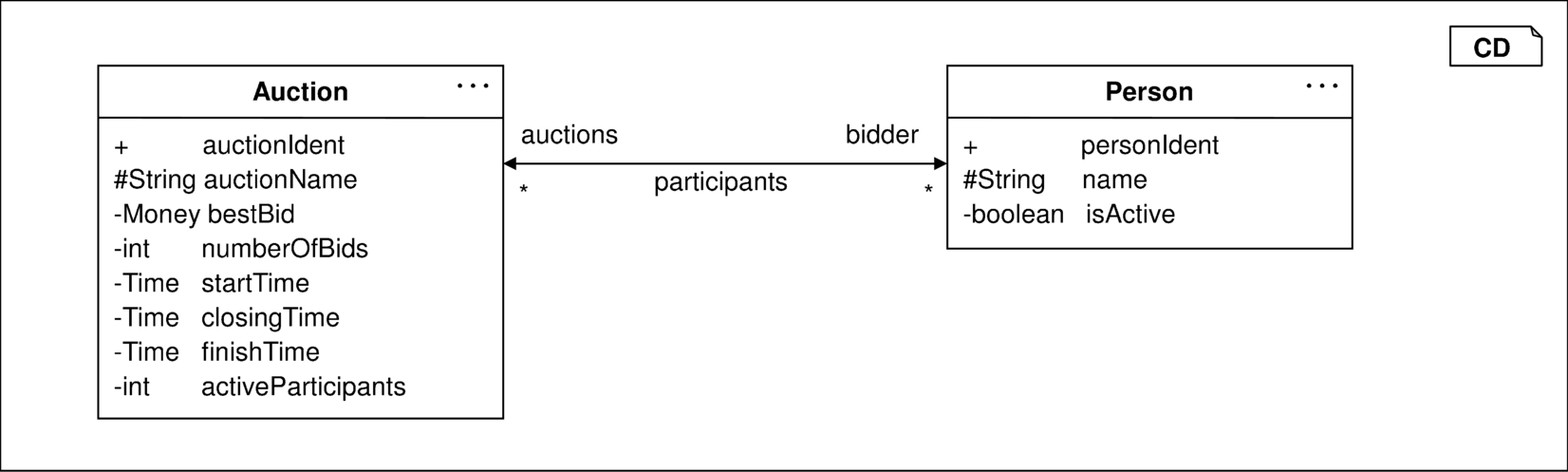
Eines der herausragenden Merkmale von OCL-Bedingungen ist ihre grundsätzliche Einbettung in einen Kontext, bestehend aus UML-Modellen. Das Klassendiagramm in Abbildung 3.11 stellt einen solchen Kontext bereit, in dem zum Beispiel folgende Aussage formuliert werden kann:
OCL  |
| context Auction a inv Bidders2: |
| a.activeParticipants == { p in a.bidder | p.isActive }.size |
Die Aussage mit dem Namen Bidders2 wird quantifiziert über alle Objekte a der Klasse Auktion. Darin enthalten sind
Navigationsausdrücke wie a.bidder, die es erlauben über Assoziationen zu navigieren. Eine Mengenkomprehension {p in …| …} selektiert alle aktiven Personen einer
Auktion. Diese Mengenkomprehension ist eine komfortable Erweiterung gegenüber dem OCL-Standard. Sie wird später in mehreren Formen ausführlicher besprochen.
Wird in einem Kontext statt einem expliziten Namen nur die Klasse festgelegt, so wird implizit der Name this als vereinbart angenommen. In diesem Fall kann auf
Attribute auch ohne Objektqualifikation zugegriffen werden. Geschlossene Bedingungen besitzen einen leeren Kontext:
OCL
 inv: inv: |
| a.startTime <= Time.now() implies |
Mithilfe des let-Konstrukts können Zwischenergebnisse einer Hilfsvariablen zugewiesen werden, um diese im Rumpf des Konstrukts gegebenenfalls mehrfach zu
nutzen:
OCL
 context inv SomeArithmeticTruth: context inv SomeArithmeticTruth: |
| a<=b implies a<=middle and middle<=b |
Das let-Konstrukt kann auch dazu genutzt werden, Hilfsfunktionen zu vereinbaren:
OCL
 context Auction a inv Time2: context Auction a inv Time2: |
| let min(Time x, Time y) = (x<=y) ? x : y |
| min(a.startTime, min(a.closingTime,a.finishTime)) |
Wie bereits gesehen, kann zur Fallunterscheidung .?.:. aber auch die äquivalente Fassung if-then-else eingesetzt werden. Im
Gegensatz zur imperativen Fallunterscheidung sind immer der then- und der else-Zweig anzugeben.
Eine spezielle Form der Fallunterscheidung erlaubt die Behandlung von Typkonversionen, wie sie bei Subtyphierarchien gelegentlich auftreten. OCL/P bietet dafür eine typsichere Konstruktion
an, die eine Kombination einer Typkonversion und einer Abfrage nach dessen Konvertierbarkeit darstellt:
OCL
 |
| let Person p = (m instanceof BidMessage ? m.bidder : null) |
Zusätzlich zu einer normalen Fallunterscheidung wird im then-Zweig der Fallunterscheidung der Typ der Variable m auf den Subtyp
gesetzt und ermöglicht dadurch die Selektion m.bidder. Die Typsicherheit bleibt trotz Konversion erhalten.
Als Grunddatentypen stehen die aus Java bekannten Sorten boolean, char, int, long, float, byte, short und double und darauf arbeitende
Operatoren ohne Seiteffekte zur Verfügung. Ausgeschlossen sind damit die Inkrementoperatoren ++ und -- sowie alle Zuweisungsformen.
Neu sind die booleschen Operatoren implies und <=>, die zur Darstellung von Implikationen und Äquivalenzen dienen, und die
Postfixoperatoren @pre und ⋆⋆.
|
|
|
|
| Priorität |
Operator |
Assoziativität |
Operand(en), Bedeutung |
|
|
|
|
| 14 |
@pre |
links |
Wert des Ausdrucks in der Vorbedingung |
|
⋆⋆ |
links |
Transitive Hülle einer Assoziation |
| 13 |
+, -, ~ |
rechts |
Zahlen |
|
! |
rechts |
Boolean: Negation |
|
(type) |
rechts |
Typkonversion (Cast) |
| 12 |
⋆, /, % |
links |
Zahlen |
| 11 |
+, - |
links |
Zahlen, String (+) |
| 10 |
<<, >>, >>> |
links |
Shifts |
| 9 |
<, <=, >, >= |
links |
Vergleiche |
|
instanceof |
links |
Typvergleich |
|
in |
links |
Element von |
| 8 |
==, != |
links |
Vergleiche |
| 7 |
& |
links |
Zahlen, Boolean: striktes und |
| 6 |
^ |
links |
Zahlen, Boolean: xor |
| 5 |
| |
links |
Zahlen, Boolean: striktes oder |
| 4 |
&& |
links |
Boolesche Logik: und |
| 3 |
|| |
links |
Boolesche Logik: oder |
| 2,7 |
implies |
links |
Boolesche Logik: impliziert |
| 2,3 |
<=> |
links |
Boolesche Logik: äquivalent |
| 2 |
? : |
rechts |
Auswahlausdruck (if-then-else) |
|
|
|
|
Tabelle 3.12: Prioritäten der OCL-Operatoren
Der Datentyp String wird wie in Java nicht als Grunddatentyp, sondern als standardmäßig zur Verfügung stehende Klasse verstanden.
3.2.2 Die OCL-Logik
Die richtige Definition der einer Bedingungssprache zugrunde liegenden Logik ist für einen praxistauglichen Einsatz der Sprache wichtig. Deshalb wurde für OCL/P eine zweiwertige Logik
und ein spezieller Umgang mit dem problematischen „Undefined“ gewählt. Eine detaillierte Diskussion dieser Aspekte ist in Band 1 zu finden.
Für die Logik ist die Abbildung des undefinierten Werts auf den Wahrheitswert false am elegantesten, weil damit eine zweiwertige Logik entsteht. Sowohl
Spezifikationen als auch Beweisführungen werden dadurch besonders einfach, weil ein dritter Fall nicht existiert. Unglücklicherweise ist diese, für die Spezifikation so angenehme
Semantik nicht vollständig implementierbar, da zu bestimmen wäre, ob eine Berechnung nicht terminiert, und dann der Wert false auszugeben
wäre.
3.2.3 Container-Datenstrukturen
Container sind die Grundlage der in der OCL so wichtigen Navigation über Assoziationen. Ausgehend von einem einzelnen Objekt können durch einen Navigationsausdruck eine Menge oder eine Liste von erreichbaren Objekten beschrieben und ihren Elementen gewisse Eigenschaften zugeordnet werden. Die OCL/P bietet in Analogie
zu den Java Generics drei Typkonstruktoren für Container an (Abbildung 3.14).
Für einen Vergleich von Containern ist eine binäre Operation notwendig, die auf den Elementen einen Test auf Gleichheit durchführt. Sind die Elemente Grunddatentypen oder wieder
Container, dann wird für die Elemente der Vergleich == verwendet. Sind die Elemente aber Objekte, so wird der Vergleich equals
eingesetzt. Das entspricht einem Wertevergleich für Grunddatentypen und Container sowie normalerweise einem Vergleich der Objektidentität auf Objekten. Für spezielle Objekttypen, wie
zum Beispiel String, wird jedoch equalsüberschrieben und damit ein Wertevergleich angeboten.
Die Subtypbeziehung von Set<X> und List<X> zu Collection<X> erlaubt es analog zu den Java
Generics, für jeden beliebigen Typ X statt Werten des Typs Collection<X> Werte der Typen Set<X> oder List<X> einzusetzen.
Die Aufschreibung von Mengen und Listen basiert im Wesentlichen auf der Extension von Klassen, Mengenkomprehensionen und Navigationsausdrücken:
OCL
 Auction.size < 1700; Auction.size < 1700; |
| Set{"text",""} == {"text",""}; |
| List{'a'..'c'} == List{'a','b','c'}; |
Mengen- und Listenkomprehension
OCL/P bietet gegenüber dem OCL-Standard eine funktionalen Sprachen entlehnte reichhaltige Sammlung von Möglichkeiten zur eigenschaftsorientierten und zur aufzählenden Beschreibung
von Mengen und Listen.
Die allgemeine Syntax einer Listenkomprehension ist von der Form:
OCL
 List{ expr | characterization } List{ expr | characterization } |
Dabei werden in der Charakterisierung (rechts) auch neue Variablen definiert, die in dem Ausdruck (links) genutzt werden können. Die Charakterisierung besteht deshalb aus mehreren, durch
Kommata getrennten Generatoren, Filtern und lokalen Variablendefinitionen.
Ein Generator v in list lässt eine neue Variable v über einer Liste list variieren. Beispielsweise können so Quadratzahlen beschrieben werden:
OCL
 inv: inv: |
| List{ x⋆x | x in List{1..5} } == List{1,4,9,16,25} |
Der Filter beschreibt eine Einschränkung auf einer Liste von Elementen. Ein solcher Filter evaluiert zu einem Wahrheitswert, der darüber entscheidet, ob
ein Element in einer Liste aufgenommen ist. In Kombination mit einem Generator können so Filter für Teillisten beschrieben werden:
OCL
 inv: inv: |
| List{ x⋆x | x in List{1..8}, !even(x) } == List{1,9,25,49} |
Zur weiteren Unterstützung des Beschreibungskomforts können Zwischenergebnisse berechnet und lokalen Variablen zugewiesen werden.
OCL
 inv: inv: |
| List{ y | x in List{1..8}, int y = x⋆x, !even(y) } == |
Container-Operationen
Mengen, Listen und Container allgemein besitzen die in den Abbildungen 3.15, 3.16 und
3.17 aufgelisteten Operationen. Deren Signatur stellt eine Integration der aus der Java-Realisierung von Mengen bekannten und der vom
OCL-Standard angebotenen Funktionalität dar. Die Operationen size, isEmpty und asList können in OCL
wie Attribute ohne Klammern geschrieben werden, denn eine Query ohne Argumente kann grundsätzlich wie ein Attribut behandelt werden. Eine Schreibweise als Query mit Klammern ist wegen der
Kompatibilität zu Java ebenfalls möglich.
Im Gegensatz zu einer Java-Implementierung ist für OCL-Ausdrücke das Konzept der Exceptions nicht vorhanden. Stattdessen sind alle Operatoren der OCL robust, so dass ihre Interpretation immer sinnvolle Ergebnisse ergibt.
Weil in der OCL Container keine Objektidentität besitzen, sind auf Containern beide Gleichheits-Operatoren == und equals
identisch:
OCL
 context Set<X> sa, Set<X> sb inv: context Set<X> sa, Set<X> sb inv: |
Bei dem Vergleich von Mengen wird, wie bereits besprochen, auf den Vergleich der Elemente equals für Objekte und == für
Grunddatentypen zurückgegriffen. In der OCL ist == für Container von Objekten von der frei definierbaren Gleichheit equals auf
den Elementen abhängig und unterscheidet sich von dem Vergleich in Java.
Für den praktischen Einsatz angenehm, da systematischer, ist die aus Java bekannte Indizierung der Listenelemente beginnend mit 0:
OCL
List{0,1,2}.add(3) == List{0,1,2,3}; |
| List{'a','b','c'}.add(1,'d') == List{'a','d','b','c'}; |
| List{0,1,2}.prepend(3) == List{3,0,1,2}; |
| List{0,1,2}.set(1,3) == List{0,3,2}; |
| List{0,1,2}.rest == List{1,2}; |
| List{0,1,2,1}.remove(1) == List{0,2}; |
| List{0,1,2,3}.removeAtIndex(1) == List{0,2,3}; |
| List{0,1,2,3,2,1}.removeAll(List{1,2}) == List{0,3}; |
| List{0..4}.subList(1,3) == List{1,2}; |
Tief geschachtelte Container-Strukturen enthalten eine gewisse Strukturierungsinformation, die in manchen Fällen zur Spezifikation von Systemen hilfreich ist. So kann mit dem Typ
Set<Set<Person>> eine Gruppierung von Mengen von Personen beschrieben werden.
OCL
 let Set<Set<Person>> ssp = { a.bidder | a in Auction } let Set<Set<Person>> ssp = { a.bidder | a in Auction } |
Der Operator flatten erlaubt es, solche Container-Strukturen größerer Schachtelungstiefe flach zu drücken.
Der flatten-Operator verschmilzt die beiden „oberen“ Ebenen von Containern, ohne sich um die interne Struktur des darin verborgenen Elementtyps
X zu kümmern. Man spricht auch von schmalem (engl.: shallow) Flachdrücken. Eine genaue
Beschreibung dazu ist in Band 1 zu finden.
Bei Navigationsketten wird der flatten-Operator implizit eingesetzt, so dass das Ergebnis einer Navigationskette nie eine Container-Struktur darstellt, die tiefer
verschachtelt ist als die Ausgangsstruktur. Einzige Ausnahme bildet die Navigationskette ausgehend von einem einzelnen Objekt, die je nach Form der Assoziation zu einer Menge oder Sequenz
führen kann.
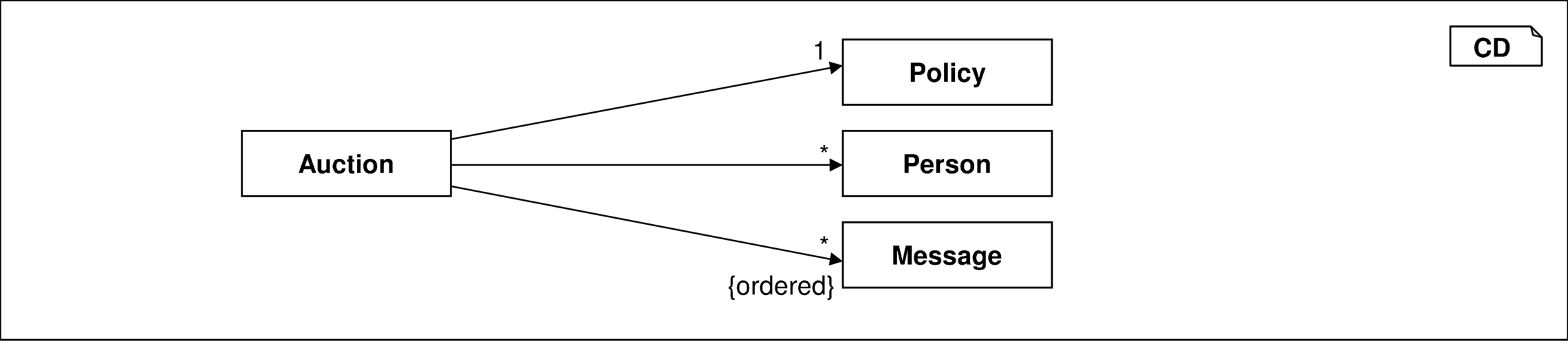
Ausgehend von einem einfachen Objekt hängt das Ergebnis von der Kardinalität der Assoziation gemäß Abbildung 3.18
ab:
OCL
 let Auction a
= ...; let Auction a
= ...; |
| Set<Person> spe = a.person; |
| List<Message> lm = a.message |
Quantoren und spezielle Operationen
Die beiden Quantoren forall und exists erlauben die Beschreibung einer Eigenschaft, über alle Elemente einer Gruppe beziehungsweise
wenigstens einem der Elemente. In einigen vorhergehenden Beispielen wurde bereits gezeigt, wie Quantoren eingesetzt werden, um über die Elemente eines Containers Aussagen zu formulieren.
Quantoren können über mehrere Variablen kombiniert werden:
OCL
 inv Nachrichten1: inv Nachrichten1: |
| forall a in Auction, p in Person, m in a.message: |
| p in a.bidder implies m in p.message |
Der dritte Quantor dieses Beispiels zeigt, dass die Ausgangsmenge, über die quantifiziert wird, nicht nur die Extension einer Klasse, sondern ein beliebiger mengen- oder listenwertiger
Ausdruck sein kann.
Der Existenzquantor ist dual zum Allquantor:
OCL
 inv: inv: |
| (exists var in setExpr: expr) <=> |
| !(forall var in setExpr: !expr) |
Beide Quantoren werden meist nur auf endliche Container oder Extensionen angewandt. Dies hat den Vorteil der (zumindest prinzipiellen) Berechenbarkeit, indem die quantifizierte Variable mit
allen Werten beziehungsweise Objekten belegt und der Rumpf damit interpretiert wird. Für die quantifizierte Menge ist wesentlich, dass den Klassen, wie zum Beispiel Person, die Extension in Form aller aktuell existierenden Objekte zugeordnet wird, die zwar unbeschränkt aber zu jedem Zeitpunkt endlich ist.
Neben endlichen Mengen von Objekten erlaubt die OCL/P auch die Benutzung von Quantoren über unendlichen Grunddatentypen wie zum Beispiel int und ist hier
natürlich unberechenbar. Bei Mengen und Listen wird ebenfalls über potentielle (und nicht die gerade im System befindlichen Mengen-Implementierungen) quantifiziert. Die Aussage
OCL
 inv ListQuantor: inv ListQuantor: |
| forall Set<Person> lp: lp.size != 5 |
interpretiert die Variable lp über alle potentiellen Listen über die tatsächlich zu einem Zeitpunkt
existierenden Objekte. Damit ist eine Quantifizierung über Set<Person> eine Kombination der Interpretation eines unendlichen Quantors auf einem Grunddatentyp
und einem endlichen Quantor über den darin befindlichen Referenztyp. Entsprechend sind Quantoren über Listen unendlich und können daher nur zur Spezifikation eingesetzt werden. Da
die Potenzmenge einer endlichen Menge ebenfalls endlich ist, ist die obige Quantifizierung über Set<Person> endlich und sogar erfüllbar.
Für die Selektion eines Elements aus einer Container-Struktur gibt es den speziellen Operator any. Dieser Operator ist für Mengen nicht eindeutig
festgelegt, wie die folgenden definierenden Gleichungen zeigen:
OCL
(any listExpr) == listExpr.get(0); |
| (any setExpr) == any setExpr.asList; |
| (any var in collection: expr) == any { var in collection | expr } |
Für eine elementweise Bearbeitung von Mengen und Listen gibt es neben den Komprehensionsformen den iterate-Operator, der eine Schleife mit
Zustandsspeicher aus der funktionalen wie auch der imperativen Programmierung nachbildet:
OCL
 iterate { elementVar in setExpr; iterate { elementVar in setExpr; |
| Type accumulatorVar = initExpr : |
Der iterate-Operator kann zum Beispiel eingesetzt werden, um die Summe einer Menge von Zahlen zu berechnen:
OCL
 inv Summe: inv Summe: |
| iterate { elem in Auction; |
| acc = acc+elem.numberOfBids |
Für die Behandlung undefinierter Werte wird der defined-Operator eingeführt, der genau dann true liefert, wenn
sein Argument definiert ist. Für undefinierte Argumente evaluiert dieser Operator zu false:
OCL
 context Auction a inv: context Auction a inv: |
| let Message mess = a.person.message[0] |
| defined(mess) implies ... |
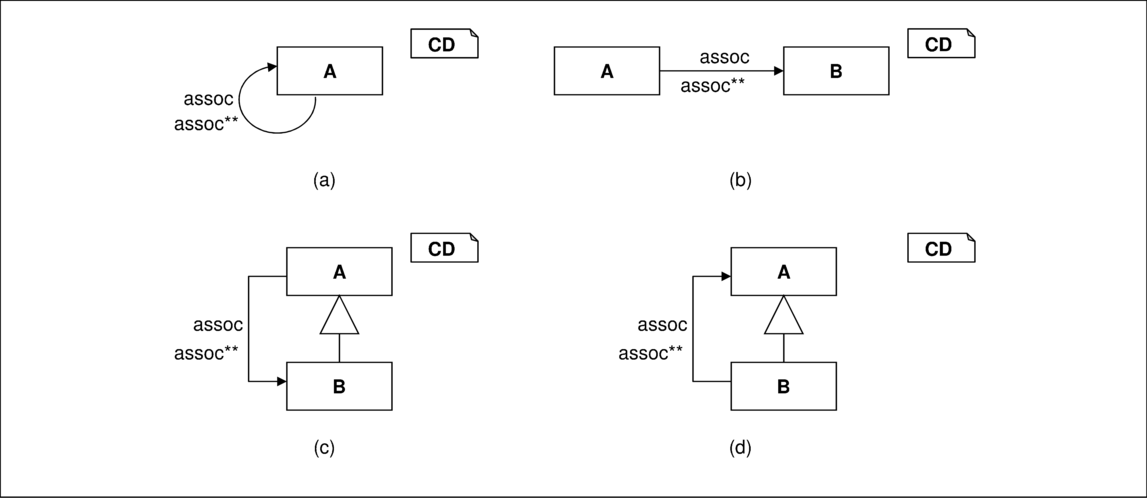
Ein ganz spezifisches Problem der OCL stellt die Definition transitiver Hüllen über Navigationswege dar: OCL ist eine Logik erster Ordnung und daher nicht in der Lage,
eine transitive Hülle zu spezifizieren. Deshalb existiert in OCL/P ein spezieller Operator ⋆⋆, der auf eine Asssoziation angewandt deren Signatur
beibehält. In Kombination mit Vererbung gibt es deshalb die vier in Abbildung 3.19 angegebenen Fälle.
3.2.4 Funktionen in OCL
Mithilfe von Paaren aus Vor- und Nachbedingung können einerseits die Effekte von Methoden des zugrunde liegenden Modells spezifiziert werden. Umgekehrt kann das Modell Methoden für die
Spezifikation von OCL-Bedingungen zur Verfügung stellen. Eine solche Methode wird Query genannt und wird durch den Stereotyp ≪query≫ gekennzeichnet. Queries sind seiteneffektfrei im Sinne der in Band 1 beschriebenen Form.
Für die Modellierung komplexer Eigenschaften ist es oft sinnvoll oder sogar notwendig, zusätzliche Queries zu definieren, die jedoch nicht implementiert werden. Solche Spezifikationsqueries werden mit dem Stereotyp ≪OCL≫ gekennzeichnet.
Methodenspezifikation
Für die Beschreibung einzelner Methoden wird eine Methodenspezifikation eingesetzt, die im Vor-/Nachbedingungstil formuliert wird.
Der Kontext einer Methodenspezifikation wird durch eine Methode, der sie beinhaltenden Klasse sowie den zugehörigen Parametern festgelegt. Zwei Bedingungen, die Vorbedingung und die Nachbedingung, die beide mit Namen versehen werden können, charakterisieren den Effekt der Methode.
Die Vorbedingung beschreibt, unter welchen Bedingungen eine Methode aufgerufen werden kann, so dass eine definierte und robust implementierte Reaktion entsteht. Die Nachbedingung charakterisiert
das Ergebnis des Methodenaufrufs und die Veränderungen auf dem Objektzustand.
Das Methodenergebnis wird in der Nachbedingung mit result bezeichnet. Statische Methoden werden mit ≪static≫ markiert. In ihrem Rumpf darf wie bei einer Implementierung kein this eingesetzt werden.
Die Nachbedingung der Methodenspezifikation kann einen expliziten Bezug auf den Zustand vor dem Methodenaufruf durch Verwendung des Postfix @pre enthalten. Methode
addMessage aus Abbildung 3.20, dient dazu, bei einer Person eine weitere Nachricht hinzuzufügen:
OCL
 context Person.addMessage(Message m) context Person.addMessage(Message m) |
| pre: m.time >= messageList.last.time |
| post: messageList == messageList@pre.add(m) |
Der Operator @pre darf nur auf einzelne Attribute oder Navigationselemente angewandt werden. a@pre evaluiert zu dem Wert
des Attributs a zur Zeit des Methodenaufrufs und erlaubt so den Vergleich zwischen altem und neuen Wert.
Ist die Vorbedingung nicht erfüllt, so ist mit der Spezifikation über das Verhalten der Methode nichts ausgesagt. Deshalb ist es möglich eine komplexe Methode durch mehrere
Spezifikationen zu beschreiben. Es wird festgelegt, dass bei überlappenden Vorbedingungen beide Nachbedingungen zu erfüllen sind. Mit dieser Kompositionstechnik lassen sich
Methodenspezifikationen sogar vererben und in Subklassen spezialisieren. Details dazu lassen sich in Band 1 finden.
Für komplexe Methodenspezifikationen existiert eine erweiterte Form des let-Konstrukts, das es erlaubt Variablen zu definieren, die in beiden Bedingungen belegt
sind:
OCL
 context Class.method(parameters) context Class.method(parameters) |
Rekursive Funktionsdefinitionen sind erlaubt, aber wie in Band 1 diskutiert nur sehr restriktiv einzusetzen.
Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012

 inv:
inv: context inv SomeArithmeticTruth:
context inv SomeArithmeticTruth: context Auction a inv Time2:
context Auction a inv Time2:
 Auction.size < 1700;
Auction.size < 1700; List{ expr | characterization }
List{ expr | characterization } inv:
inv: inv:
inv: inv:
inv: context Set<X> sa, Set<X> sb inv:
context Set<X> sa, Set<X> sb inv:
 let Set<Set<Person>> ssp = { a.bidder | a in Auction }
let Set<Set<Person>> ssp = { a.bidder | a in Auction } let Auction a
= ...;
let Auction a
= ...; inv Nachrichten1:
inv Nachrichten1: inv:
inv: inv ListQuantor:
inv ListQuantor: iterate { elementVar in setExpr;
iterate { elementVar in setExpr; inv Summe:
inv Summe: context Auction a inv:
context Auction a inv: context Person.addMessage(Message m)
context Person.addMessage(Message m) context Class.method(parameters)
context Class.method(parameters)