6.3 Semantik eines Sequenzdiagramms

Auf den exemplarischen Charakter eines Sequenzdiagramms wurde bereits hingewiesen. Für den methodisch einwandfreien Einsatz von Sequenzdiagrammen ist jedoch eine genauere Erklärung der Bedeutung eines solchen exemplarischen Ablaufs und des Umgangs mit unvollständigen Darstellungen notwendig.

Exemplarizität und Unvollständigkeit

Die Exemplarizität eines Sequenzdiagramms basiert analog zum Objektdiagramm auf der Beschreibung einer Menge von Objekten, die in dieser Form in beliebiger Häufigkeit oder auch gar nicht, in einem System auftreten kann. Außerdem ist der Ablauf an sich exemplarisch, der in dieser Form sogar beliebig häufig nebeneinander und verschachtelt, aber auch gar nicht auftreten kann.

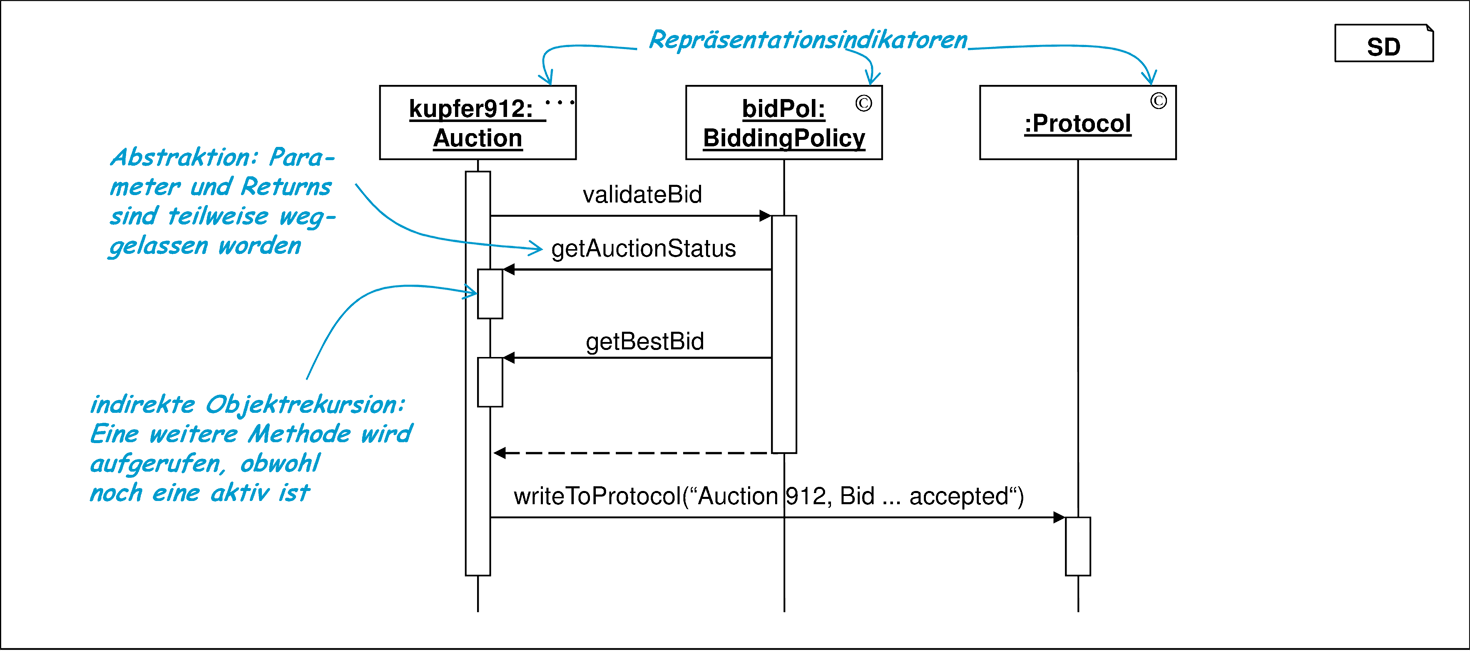
Zu diesen Formen der Exemplarizität kommt hinzu, dass ein Sequenzdiagramm eine Abstraktion eines Ablaufs darstellt, da es weder alle Objekte des Systems, noch alle auftretenden Interaktionen beinhalten kann. Bei einem Sequenzdiagramm können auch zwischendurch Interaktionen fehlen. So kann Abbildung 6.9 eine Darstellung desselben Ablaufs wie Abbildung 6.8 auf einer anderen Abstraktionsstufe darstellen, da teilweise andere Objekte gezeigt werden.

Abbildung 6.9: Darstellung mit anderer Abstraktionsstufe

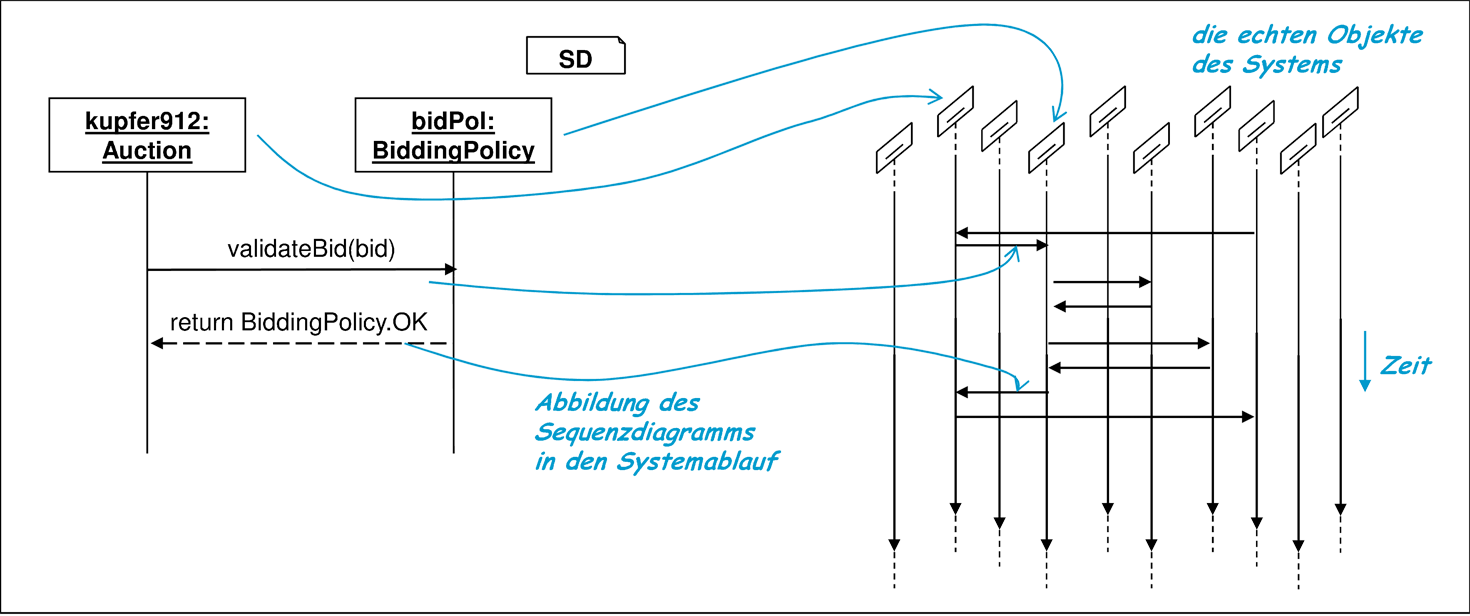
Formal kann die Bedeutung eines Sequenzdiagramms durch eine Abbildung der Elemente des Diagramms in einem Systemablauf erklärt werden. Die Illustration 6.10 zeigt eine solche Abbildung, wobei für den Systemablauf auf der rechten Seite eine Darstellung verwendet wurde, die einem Sequenzdiagramm ähnlich ist und die analog zu Abbildung 3.19 verstanden werden kann.

Abbildung 6.10: Abbildung eines Sequenzdiagramms in einen Systemablauf

Diese Abbildung identifiziert die im Sequenzdiagramm auftretenden prototypischen Objekte mit echten Objekten und die dargestellten Interaktionen mit echten Interaktionen des Systems. Dabei muss die zeitliche Reihenfolge eingehalten werden. Diese Form des Matchings entspricht der bereits früher diskutierten Form des Beobachters, der selektiv Objekte beobachtet und manche Interaktionen protokolliert. Mit mathematischen Mitteln kann diese Abbildung zum Beispiel wie in den Abbildungen 6.11 und 6.12 beschrieben werden.

Eine lose Semantikdefinition für Sequenzdiagramme wird durch die Abbildung der Elemente eines Sequenzdiagramms auf die Elemente eines Systemablaufs beschrieben. Die Essenz eines Sequenzdiagramms ist gegeben durch

• die Menge der prototypischen Objekte O,
• die Menge von möglichen Diagramm-Interaktionen A,
• die Zuordnung der Quelle jeder Interaktion q : A →O,
• die Zuordnung des Ziels jeder Interaktion z : A →O und
• eine Sequenz von Diagramm-Interaktionen s ∈ A^*, wobei mehrfaches Auftreten derselben Interaktion erlaubt ist.

Die Essenz eines Systemablaufs besteht in ähnlicher Weise aus einer Menge von Objekten Obj , von Interaktionen Act, zwei Abbildungen q,z : Act → Obj für Quelle und Ziel jeder Interaktion und des Systemablaufs s ∈ Act^*, der einen Trace [DR95] darstellt. Nach [Rum96] kann die Dynamik der Objekterzeugung durch eine vorgegebene Objektmenge simuliert und damit hier ignoriert werden.

Seien Ix_s = {0..n} die n + 1 Indizes der Sequenz s = s₀s₁…s_n und s_i das Element an Position i ∈ Ix_s.

Die Zuordnung erfolgt nun durch die Forderung nach der Existenz einer Abbildung für Objekte f : O → Obj und einer monoton steigenden Injektion j : Ix_s → Ix_s der Indizes von s in die Indizes von s. Es muss für jeden Index i ∈ Ix_s im Sequenzdiagramm gelten:

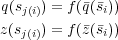
Monotonie und Injektivität von j sichern die zeitliche Reihenfolge der Abbildung. Ein Sequenzdiagramm bildet eine Abstraktion des Systemablaufs, da für f und j keine Surjektivität gefordert ist.

Abbildung 6.11: Lose Semantik für Sequenzdiagramme, Teil 1

Die lose Semantikdefinition für Sequenzdiagramme aus Abbildung 6.11 wird um die Zuordnung zwischen Returns und Aufrufen detailliert. Die Essenz eines Sequenzdiagramms wird dafür um

• die Menge der Returns und Exceptions R ⊆A und
• die Zuordnung der Returns an die jeweiligen Methodenaufrufe m : R → (A \R)

erweitert. Analog wird die Darstellung eines Systemablaufs durch Returns und Exceptions R ⊆ Act und der bijektiven Zuordnung m : R → (Act \R) erweitert. m ist eine Bijektion. Aufgrund der Unvollständigkeit eines Sequenzdiagramms muss m nur injektiv und vollständig definiert sein.

Es gilt für jedes Paar von Indizes r,a ∈ Ix_s:

Abbildung 6.12: Lose Semantik für Sequenzdiagramme, Teil 2

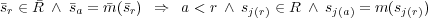
Mehrdeutigkeit und einschränkende Stereotypen

Bei der in den Abbildungen 6.11 und 6.12 beschriebenen Form des Matchings können jedoch mehrere Zuordnungen möglich sein. Findet ein Methodenaufruf im System während des Beobachtungszeitraums mehrfach statt, so ist offen, welcher tatsächliche Methodenaufruf mit der im Diagramm dargestellten Interaktion korrespondiert. Der fiktive Beobachter hat gegebenenfalls einzelne Interaktionen zwischen beiden Objekten „übersehen“.

Mithilfe geeigneter Stereotypen kann jedoch die Beobachtungsform genauer festgelegt werden. Der Repräsentationsindikator „©“ kann bei Objekten im Sequenzdiagramm eingesetzt werden, um die Vollständigkeit der gezeigten Interaktionen anzuzeigen. Der alternative Repräsentationsindikator „…“ für Unvollständigkeit gilt bereits per Default, kann aber ebenfalls explizit angegeben werden. Abbildung 6.9 zeigt die Anwendung der Indikatoren. Ein „©“ bedeutet, dass zwischen der ersten und der letzten im Diagramm dargestellten Interaktion keine andere Interaktion des markierten Objekts mit irgendeinem Objekt stattfindet. Das heißt, das Protokoll des fiktiven Beobachters ist in Bezug auf das markierte Objekt und den dargestellten Beobachtungszeitraum vollständig.

Bei einem in diesem Sinn vollständig beobachteten Objekt ergibt sich notwendigerweise, dass zu jedem Aufruf ein passender Return angegeben sein muss. Dabei sind alle Objekte anzugeben, die direkt mit dem beobachteten Objekt interagieren. Dies kann zu erheblich detaillierteren Diagrammen führen, als eigentlich gewünscht wird. Deshalb werden weitere Stereotypen verwendet, die zusätzliche Varianten der Semantikdefinition erlauben.

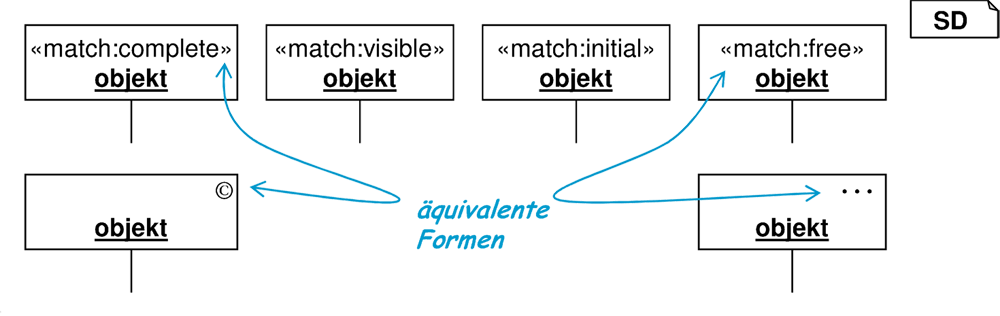
Der Stereotyp ≪match:initial≫ ist zum Beispiel besonders gut geeignet für die Definition von testbaren Sequenzdiagrammen, während die freie Interpretation ≪match:free≫ dem Default „...“ entspricht. Tabelle 6.13 beschreibt die vier unterschiedlichen Varianten. Weitere Varianten, die die Form der Beobachtung weiter verfeinern, sind denkbar. So könnten Listen von Methodenaufrufen explizit angegeben werden, die vollständig beobachtet oder ignoriert werden. Dies würde aber die Informationsdichte eines Sequenzdiagramms so erhöhen, dass es schwerer lesbar wird.

Eine formale Definition der vier Varianten ist auf Basis regulärer Ausdrücke in Abbildung 6.14 gegeben. Dabei wird der gesamte Ablauf eines Systems als Wort und ein Sequenzdiagramm als ein regulärer Ausdruck verstanden, für den übereinstimmende Stellen im Systemablauf gesucht werden.

Die lose Semantikdefinition für die Stereotypen ≪match:*≫ basiert auf den Grundlagen aus Abbildung 6.11. Vereinfachend sei hier angenommen, dass A ⊆ Act und O ⊆ Obj , dass von den Argumenten der Interaktionen abstrahiert wird und f die Identität ist. Es sei außerdem obj(a) = {q(a),z(a)}.

Jedes Objekt in O ist mit einem der Stereotypen markiert. Sei jeweils O_ϕ ⊆ O die Menge, der mit ≪match:ϕ≫ gekennzeichneten Objekte des Sequenzdiagramms.

Ein Systemablauf kann als Wort über dem Alphabet der Interaktionen Act aufgefasst werden. Einem Sequenzdiagramm wird als Semantik ein regulärer Ausdruck zugeordnet, dem Systemabläufe genügen. Dies lässt sich nutzen, um im Folgenden die Semantik der ≪match:*≫-Stereotypen zu erklären.

Das Sequenzdiagramm s = a₀a₁a₂…a_n bestehend aus den n + 1 Interaktionen a_k ∈ Act kann zu einem regulären Ausdruck umgebaut werden. Dieser nimmt die Form

an, der eine Menge von Systemabläufen beschreibt. Vor der ersten und nach der letzten beschriebenen Interaktion ist der Systemablauf nicht eingeschränkt. Die Menge der möglichen Interaktionen in X_k hängt von den gewählten ≪match:*≫-Stereotypen ab. Folgende Interaktionen sind jeweils verboten:

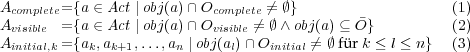
(1) und (2) beschreiben Interaktionen, die im Sequenzdiagramm angegeben sein müssten und daher zwischendurch verboten sind. (3) identifiziert Interaktionen, die im Sequenzdiagramm später noch angegeben sind und daher dem initialen Matching widersprechen.

Es gilt X_k = Act \ A_complete \ A_visible \ A_initial,k.

Die Argumente von Interaktionen Act können durch Einführung einer Typisierung berücksichtigt werden. Ebenfalls berücksichtigt werden kann die zum Objektdiagramm analoge dynamische Zuordnung der prototypischen Objekte zu echten Objekten.

Abbildung 6.14: Semantik der Stereotypen ≪match:*≫

Einer der großen Vorteile der Äquivalenz dieser Formalisierung zu regulären Ausdrücken ist, dass es effiziente Verfahren aus der Theorie formaler Sprachen gibt, die Systemabläufe protokollieren und auftretende Matches erkennen können. Dies ist eine wesentliche Voraussetzung des Einsatzes von Sequenzdiagrammen für Tests. Allerdings erleidet diese Effizienz Einbußen, wenn zwischendurch Variablen belegt und OCL-Bedingungen ausgewertet werden müssen.

Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012