B. Rumpe: Modellierung mit UML

<< zurück

weiter >>

3.5 Ausdrucksmächtigkeit der OCL

Um die OCL erfolgreich einzusetzen, ist es sinnvoll, zu verstehen was mit der OCL nicht oder zumindest nicht adäquat beschrieben werden kann. Auch ist die Natur einer Invariante in objektorientierten Systemabläufen und ihr Einsatzgebiet genauer zu klären. Zur Untersuchung der Ausdrucksmächtigkeit einer Sprache gehört auch die Frage nach der Ausführbarkeit. Ein Vergleich mit einer vollständigen Spezifikationssprache wie Spectrum [BFG⁺93] gibt weiteren Aufschluss über die Fähigkeiten der OCL.

3.5.1 Transitive Hülle

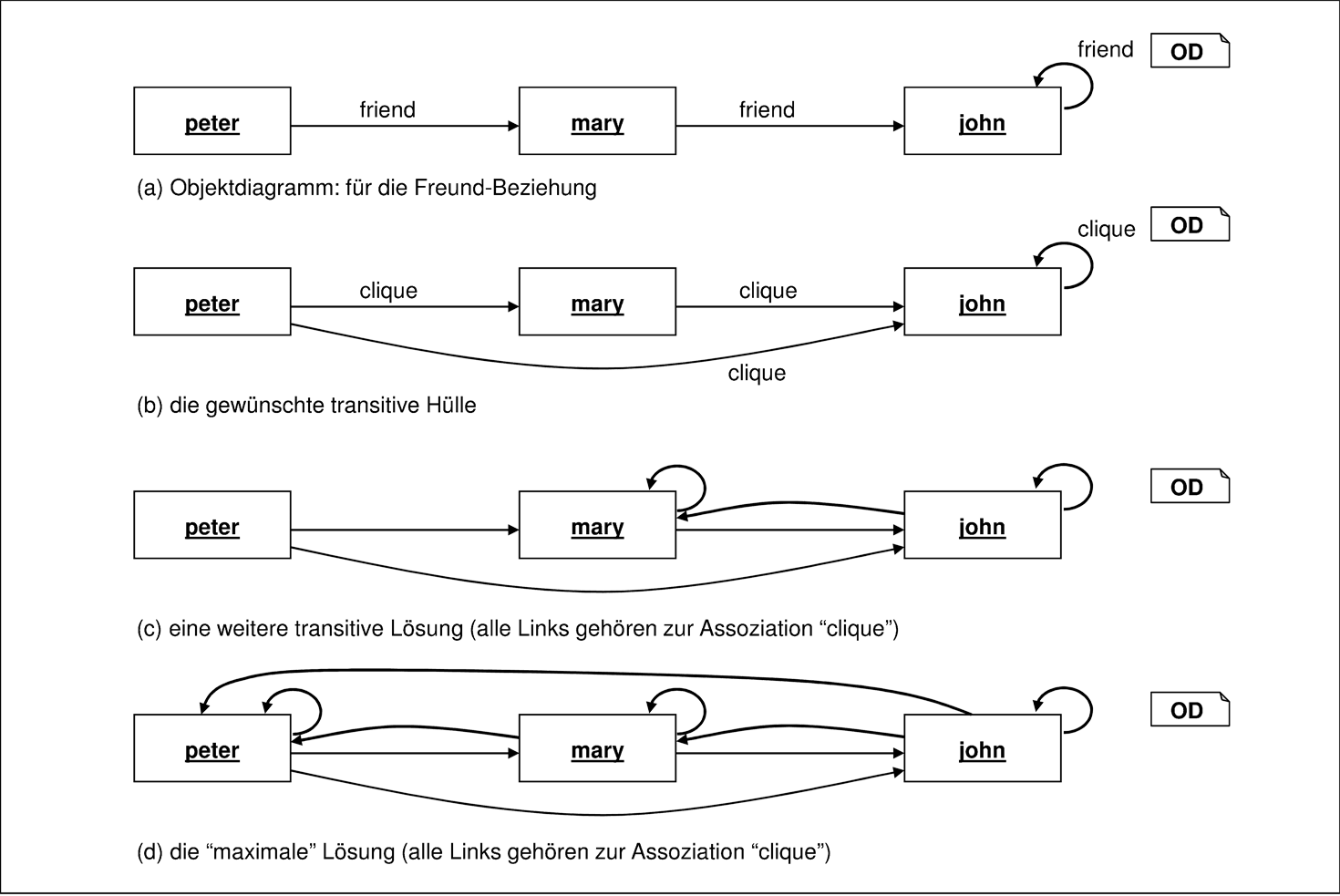
Ein beliebtes Beispiel zur Demonstration der Fähigkeiten der OCL ist die Modellierung der transitiven Hülle einer binären Relation. Als Basisrelation wird dazu eine selbstbezügliche Assoziation aus dem zugrunde liegenden Modell verwendet. Die in einer Komposition verwendete Teile-Ganzes-Beziehung ist dafür ein typisches Beispiel. Ein weiteres Beispiel ist die transitive Hülle der Vererbungsbeziehung, die im UML-Standard [OMG10b] zur Modellierung der Kontextbedingungen auf Ebene des Metamodells eingesetzt wird. Abbildung 3.32 zeigt die Klasse Person, von der im System ebenfalls Freunde gespeichert werden können. Die abgeleitete Assoziation clique soll nun so spezifiziert werden, dass sie die transitive Hülle der friend-Assoziation darstellt und damit die Menge aller Vorfahren direkt zugreifbar macht.

Abbildung 3.32: Reflexive Assoziation und transitive Hülle

Die transitive Hülle wird in den vorgenannten Beispielen nach folgendem Muster spezifiziert:

context Person inv Transitiv:
clique = friend.addAll(friend.clique)

Leider ist diese Spezifikation unvollständig. Sie stellt zwar sicher, dass die Assoziation clique eine Obermenge der Assoziation friend ist und dass die Assoziation transitiv ist, aber es gibt eine Vielzahl weiterer Realisierungen für die clique-Assoziation. Abbildung 3.33(a) zeigt eine Objektstruktur mit drei Objekten und der Assoziation friend, für die in 3.33(b-d) mehrere Lösungen für die Invariante Transitiv angegeben sind.

Abbildung 3.33: Lösungen für die transitive Hülle

Insgesamt gibt es für die in Abbildung 3.33(a) beschriebene Situation elf Lösungen. Beschrieben werden sollte aber nur eine. Die gewünschte Lösung hat ein wesentliches Charakteristikum gegenüber allen anderen Lösungen: Sie ist in allen Lösungen enthalten, also die Minimallösung. Würde die Bedingung Transitiv als Logikprogramm aufgefasst, so würde genau die Minimallösung berechnet werden. Die Minimalität der gewünschten Lösung korrespondiert also mit der Interpretation der Bedingung als Berechnungsvorschrift. Jedoch ist die OCL keine Programmier- sondern eine eigenschaftsorientierte Spezifikationssprache. Die Problematik in dieser Charakterisierung ist die darin eingebettete Rekursion: Sie benutzt die Assoziation clique bereits für deren Definition. Eine derartige rekursive Situation sollte in Spezifikationen soweit wie möglich vermieden werden, da sie immer wieder zu Problemen führt. Auch eine eine Variante, die die transitive Hülle in Methodenform definiert, hat diesselbe Vielfalt an Implementierungsmöglichkeiten:

context Person.clique() inv Transitiv2:
post: result = friend.addAll(friend.clique())

Mithilfe der in der Fixpunkttheorie lässt sich die Minimalitätseigenschaft der transitiven Hülle elegant für die eindeutige Charakterisierung nutzen. OCL ist jedoch nur eine Logiksprache erster Ordnung und bietet solche Konzepte nicht (direkt) an. Es gibt jedoch einen Trick, der in der OCL verwendet werden kann, um Operationen zweiter Ordnung, wie induktive beziehungsweise rekursive Strukturen, transitive Hüllen, Termerzeugung, etc. zu beschreiben, indem die in der OCL fest definierten natürlichen Zahlen herangezogen werden. Der Vollständigkeit halber sei erwähnt, dass die natürlichen Zahlen in ihrer Charakterisierung einen induktiven Aufbau²⁶ beinhalten, der besagt, dass jede natürliche Zahl durch einen endlichen Ausdruck der Form 0+1+1+1…beschreibbar ist. Die transitive Hülle lässt sich damit durch eine Methode charakterisieren, die einen Schritt zur Berechnung der transitiven Hülle macht und die Schritte über einen natürlichzahligen Parameter mitzählt:

context ≪query≫ Set<Person> Person.cliqueUpToN(int n):
post: result == if (n<1) friend
else friend.addAll(friend.cliqueUpToN(n-1))

Die Assoziation clique kann nun festgelegt werden, indem eine ausreichende Anzahl von Schritten charakterisiert wird. Die Anzahl aller beteiligten Objekte ist eine geeignete Obergrenze.

context Person inv Transitiv:
clique = cliqueUpToN(Person.size)

Auch Sequenzen besitzen einen induktiven Aufbau und können daher zur Definition einer transitiven Hülle genutzt werden. Diese Vorgehensweise ist aber häufig eher umständlich.²⁷ Da aber speziell der Umgang mit der transitiven Hülle von reflexiven Assoziationen häufiger vorkommt, wird in der OCL/P dafür ein spezieller Operator ⋆⋆ angeboten, der die transitive Hülle charakterisiert. Die Anwendung dieses Operators erfolgt in der Form:

context Person inv Transitiv:
this.clique = this.friend**

Der Ausdruck friend⋆⋆ kann selbst als abgeleitete Assoziation angesehen und in der OCL genau in dieser Form genutzt werden, wodurch die zusätzliche Assoziation cliqueüberflüssig wird.

Der Operator ⋆⋆ wird nur direkt auf eine reflexive Assoziation²⁸ angewandt. Er kann nicht auf Ketten von Assoziationen der Form (a.b.c)⋆⋆ angewandt werden. Um dennoch über verschachtelte Assoziationen sprechen zu können, lässt sich zunächst eine abgeleitete Assoziation einführen, die aus einer Kette von Assoziationen zusammengesetzt wird.

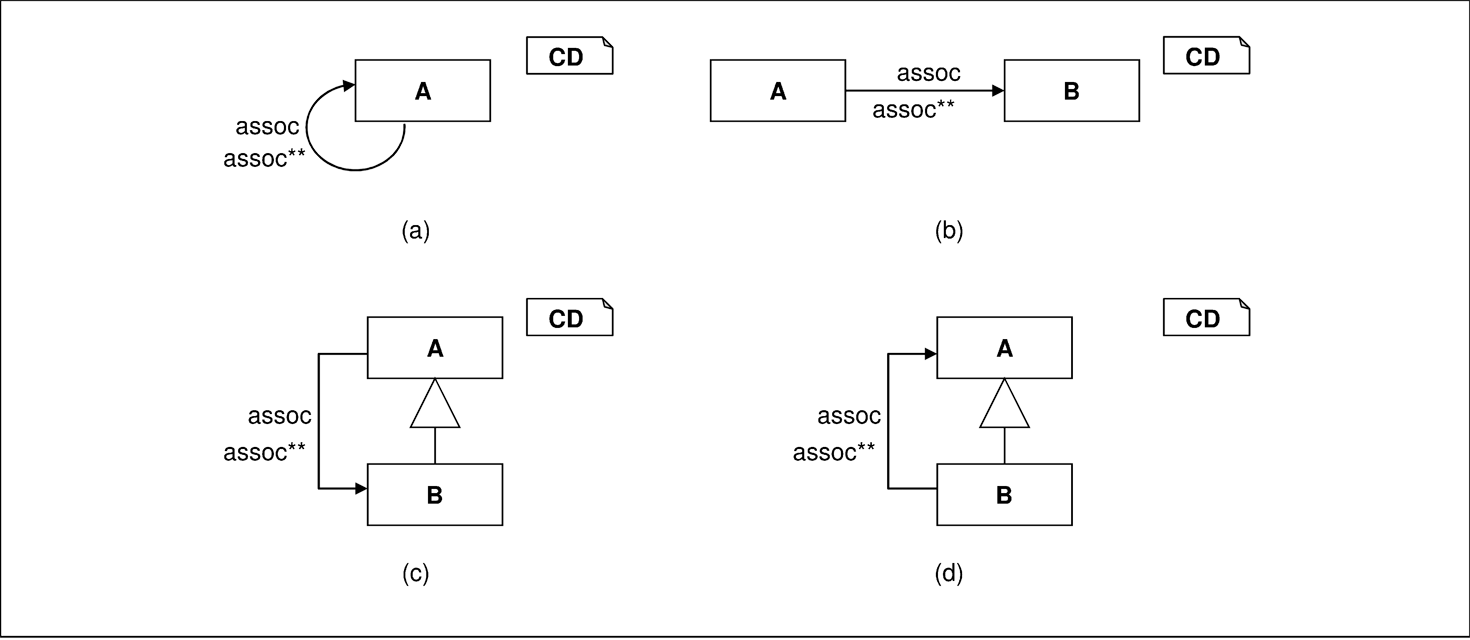
Die transitive Hülle einer Assoziation wird auch berechnet, wenn Quelle und Ziel der Assoziation nicht identisch, ja nicht einmal Unterklassen voneinander sind. Dann ist die transitive Hülle mit der Ausgangsassoziation identisch. Abbildung 3.34 illustriert, dass in allen vier auftretenden Fällen die transitive Hülle dieselbe Quell- und Zielklasse wie die Ausgangsassoziation hat. Jedoch ist bei der transitiven Hülle die Kardinalität immer „⋆“ (nicht im Bild gezeigt).

Abbildung 3.34: Typisierung der transitiven Hülle

Die transitive Hülle und eine Reihe ähnlicher Konstruktionen können durch Funktionen höherer Ordnung ebenfalls elegant modelliert werden. Funktionen höherer Ordnung sind Funktionen, die andere Funktionen als Argumente haben. In der objektorientierten Programmierung und Modellierung und deshalb auch in der OCL existieren Funktionen höherer Ordnung jedoch zurecht nicht. Stattdessen werden dort Funktionen als Methoden in Objekte gekapselt und diese Objekte als Argumente an andere Objekte weitergereicht und so Funktionen höherer Ordnung simuliert. Mehrere Entwurfsmuster, wie zum Beispiel Command [GHJV94], basieren auf diesem Prinzip. In OCL kann dieses Prinzip indirekt benutzt werden, indem geeignete Queries im Objektsystem definiert und in OCL-Bedingungen eingesetzt werden.

3.5.2 Die Natur einer Invariante

Die Bedingungen der OCL werden normalerweise als Invarianten, Vor- oder Nachbedingungen eingesetzt. Obwohl bei Invarianten ein intuitives Verständnis herrscht, dass diese zu „jedem Zeitpunkt eines Systemablaufs“ gilt, ist ein genauerer Blick auf die tatsächliche Gültigkeit einer Invariante sinnvoll.

Invarianten des Systems werden primär durch OCL-Bedingungen formuliert. Jedoch werden im nächsten Kapitel 4 auch Objektdiagramme zur Definition von Invarianten eingesetzt. Auch viele Modellierungskonzepte der Klassendiagramme lassen sich als Invarianten verstehen. Nicht direkt im Klassendiagramm ausdrückbare Erweiterungen, wie zum Beispiel Kardinalitäten von Assoziationen, können ebenfalls als Invarianten ausgedrückt werden. Eine Kardinalität der Form „3-7“ kann entsprechend durch

context object inv:
let s = object.assoziation.size
in 3 <= s && s <= 7

dargestellt werden.

Ein typisches Beispiel für eine Invariante ist die Charakterisierung einer Beziehung zwischen zwei oder mehreren Attributen. Standardbeispiel ist etwa die redundant abgelegte Länge einer Liste. Unter der Annahme, eine Klasse A habe zwei ganzzahlige Attribute x und y spezifiziert, beschreibt

context A inv Equals:
x == y

eine solche Beziehung. Wird nun ein Attribut verändert, so ist das zweite entsprechend nachzuziehen. Beispielsweise kann dies mit

void incX() {
  x++;
  // (1)
  y++;
}

erfolgen. Aufgrund der Invariante Equals dürfen und sollen sich Entwickler darauf verlassen, dass die Werte beider Attribute tatsächlich übereinstimmen. Da Java nicht die Möglichkeit besitzt, mehrere Attributänderungen atomar durchzuführen, gilt jedoch die Invariante nicht zu allen Zeitpunkten. Wenn nun aber anderer Code parallel dazu ausgeführt wird und Methode incX an Stelle (1) verweilt, so kann diese Verletzung tatsächlich Auswirkungen auf das Systemverhalten haben. Grundsätzlich gibt es zwei Möglichkeiten, dass fremder Code zur Ausführung kommt: Zum einen können nebenläufige Prozesse (Threads) mit dem Code interagieren. Zum anderen können Methodenaufrufe an andere Objekte an Stelle (1) eingebunden sein.

Obwohl Java kein Transaktionskonzept besitzt, kann mit der Synchronisierung von Methoden die nebenläufige Ausführung von Code gesteuert werden. In der Implementierung kann dann „vorübergehend“ eine Invariante verletzt werden, ohne dass es an anderer Stelle auffällt, da die kritische Stelle blockiert ist. Ist eine Invariante komplexer kann dies theoretisch dazu führen, dass diese permanent verletzt ist, obwohl das System korrekt funktioniert. Zum Beispiel kann die Invariante durch nebenläufige Prozesse an unterschiedlichen Stellen abwechselnd verletzt und wieder hergestellt werden.

In rein sequentiellen Systemen ohne Nebenläufigkeit kann die Kontrolle nur durch einen Methodenaufruf abgegeben werden. Während der Verletzung einer Invariante sollte daher ein Methodenaufruf nur sehr sparsam erfolgen, da die aufgerufene Methode überschrieben worden sein kann und sich daher anders verhält als erwartet. Methodenaufrufe sollten daher vor der Verletzung oder nach der Wiederherstellung der Invarianten vorgenommen werden.

Als Fazit dieser Diskussion ist festzuhalten, dass der Gültigkeitsbereich einer Invariante sich nicht über die gesamte Laufzeit eines Systems erstreckt.

Ein präziser Ansatz ist es daher, die Gültigkeit einer OCL-Bedingung im Java Code explizit festzulegen. Beispielsweise kann die Methode incX unter Verwendung einer Java-Erweiterung mit dem Schlüsselwort ocl als Invariante wie folgt formuliert werden:

void synchronized incX() {
  ocl Equals;
  x++;
  ocl x==y+1;
  y++;
  ocl Equals;
}

Die in Anhang B vorgestellte Integration von OCL-Bedingungen mit Java-Coderümpfen durch Verwendung der ocl-Anweisung für Zusicherungen kann eine Grundlage für eine Hoare-Logik für die Programmiersprache Java bilden. Die Artikel [vO01, RWH01] zeigen, dass gerade für die im Internet verbreitete und mit Sicherheitsfragestellungen konfrontierte Sprache Java ein solcher Logikkalkül sinnvoll umgesetzt werden kann. Ein weiteres hilfreiches Werkzeug ist der „Extended Static Checker for Java“ (ESC/Java) [RLNS00], der durch eine Reihe von Annotationen unter anderem erlaubt, Zusicherungen zu formulieren und diese statisch zu überprüfen. Jedoch erfordert die explizite Annotation von Code mit Zusicherungen in größeren Systemen einen erheblichen Aufwand, da an vielen Stellen Invarianten „mitzuschleppen“ sind, die erst in aufgerufenen Methoden von Relevanz sind.

Der praktische Einsatz von Invarianten erstreckt sich bei der Entwicklung auf die Formulierung von Eigenschaften, die noch zu realisieren sind, bei den Tests auf automatisiert zu überprüfende Zusicherungen sowie Invarianten im Code. Die Verwendung von Zusicherungen ist allerdings auch beim Weiterentwickeln von Modellen von Interesse, in der zum Beispiel eine alte mit einer neuen Datenstruktur in Beziehung gesetzt wird.

Bernhard Rumpe. Agile Modellierung mit UML. Springer 2012

<< zurück

MBSE Home

weiter >>